Obliczanie prawdopodobieństwa zdarzeń

Stronę tą wyświetlono już: 16042 razy

Zadanie 1

Z grupy 15 dziewczyn i 10 chłopaków wybrano trzy osoby. Jakie jest prawdopodobieństwo wyboru co najmniej jednej dziewczyny?

Rozwiązanie:

Jest to doświadczenie trujetapowe więc zbiór Ω tworzą 3-elementowe kombinacje bez powtórzeń ze zbioru 25-elementowego.

[1]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{\Omega}}=C_{25}^3=\frac{25!}{3!\cdot(25-3)!}=2300

A - zdarzenie, w którym wybrano co najmniej jedną kobietę, a więc liczebność zbioru wynosi:

[2]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{A}}=C_{15}^1\cdot C_{10}^2+C_{15}^2\cdot C_{10}^1+C_{15}^3

Jak widać zależność [2] jest dość złożona, a można ją uprościć budując zdarzenie przeciwne do zdarzenia A i korzystając ze wzoru P(A)=1-P(A').

A' - zdarzenie przeciwne do zdarzenia A, czyli takie w którym nie wylosowano żadnej dziewczyny

[3]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{A '}}=C_{10}^3=\frac{10!}{3!\cdot(10-3)!}=120

Teraz mogę obliczyć prawdopodobieństwo zdarzenia A w następujący sposób:

[4]

Zapis wyrażenia w formacie TeX-a:

P(A)=1-\frac{\overline{\overline{A '}}}{\overline{\overline{\Omega}}}=1-\frac{120}{2300}=\frac{109}{115} \approx 94\%

Prawdopodobieństwo wybrania co najmniej jednej dziewczyny wynosi w przybliżeniu 94%

Zadanie 2

W urnie znajduje się 5 kul białych i 7 kul zielonych. Losowo wybrano 4 kule. Oblicz prawdopodobieństwo wylosowania co najmniej dwóch kul zielonych.

Rozwiązanie:

Jest to doświadczenie 4-ro etapowe więc zbiór Ω tworzą cztero elementore kombinacje bez powtórzeń ze zbioru dwunasto elementowego.

[5]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{\Omega}}=C_{12}^4=\frac{12!}{4!\cdot(12-4)!}=495

A zdarzenie, w którym wylosowano co najmniej dwie kule zielone, prawdopodobieństwo takiego zdarzenia można obliczyć w następujący sposób:

[6]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{A}}=C_7^2\cdot C_5^2+C_7^3\cdot C_5^1+C_7^4

albo można się wziąć na sposób i obliczyć liczebność zdarzenia przeciwnego w nieco prostszy sposób:

[7]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{A '}}=C_7^1\cdot C_5^3+C_5^2\cdot C_{10}^1+C_{15}^3=\frac{7!}{1!\cdot(7-1)!}\cdot\frac{5!}{3!\cdot(5-3)!}+\frac{5!}{4!\cdot(5-4)!}=75

Obliczamy prawdopodobieństwo zdarzenia A:

[8]

Zapis wyrażenia w formacie TeX-a:

P(A)=1-\frac{\overline{\overline{A '}}}{\overline{\overline{\Omega}}}=1-\frac{75}{495}=\frac{28}{33} \approx 84\%

Prawdopodobieństwo wylosowania co najmniej dwóch zielonych kul wynosi w przybliżeniu 84%

Zadanie 3

Z talii 52 kart wybrano losowo 3 karty. Jakie jest prawdopodobieństwo wylosowania co najmniej jednego kiera.

Rozwiązanie:

Zdarzenie trój etapowe, więc zbiór Ω tworzą 3-elementowe kombinacje bez powtórzeń ze zbioru 52-elementowego.

[9]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{\Omega}}=C_{52}^3=\frac{52!}{3!\cdot(52-3)!}=22100

A - zdarzenie, w którym wylosowano co najmniej jednego kiera.

Buduję zdarzenie przeciwne.

A' zdarzenie, w którym nie wylosowano żadnego kiera.

[10]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{A '}}=C_{39}^3=\frac{39!}{3!\cdot(39-3)!}=9139

Prawdopodobieństwo zdarzenia A wynosi więc:

[11]

Zapis wyrażenia w formacie TeX-a:

P(A)=1-\frac{\overline{\overline{A}}}{\overline{\overline{\Omega}}}=\frac{997}{1700} \approx 58,6\%

Prawdopodobieństwo, że wylosowano co najmniej jednego kiera jest równe około 58,6%

Zadanie 4

Spośród liczb 1, 4, 5, 6, 7 losujemy kolejno bez zwracania dwie. Obliczyć prawdopodobieństwo tego, że: a) suma wylosowanych liczb jest mniejsza od dziesięciu; b) za pierwszym razem wylosowano liczbę parzystą.

Rozwiązanie:

Doświadczenie trój etapowe, w związku z czym tworzę zbiór Ω z dwuelementowych wariacji bez powtórzeń ze zbioru pięcioelementowego.

[12]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{\Omega}}=V_5^2=\frac{5!}{(5-2)!}=20

a) A - zdarzenie, w którym suma wylosowanych liczb jest mniejsza od dziesięciu. A={(1; 4) (1; 5) (1; 6) (1; 7) (5; 1) (5; 4) (6; 1) (7; 1)}, liczebność zbioru 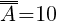overline{overline{A}}=10

Prawdopodobieństwo zdarzenia A wynosi więc:

[13]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{\overline{\overline{A}}}{\overline{\overline{\Omega}}}=\frac{10}{20}=\frac{1}{2}=50\%

b) B - zdarzenie, w którym za pierwszym razem wylosowano liczbę nieparzystą. B={(1; 4) (1; 5) (1; 6) (1; 7) (5; 1) (5; 4) (5; 6) (5; 7) (7; 1) (7; 4) (7; 5) (7; 6)}, liczebność zbioru overline{overline{B}}=12.

Prawdopodobieństwo zdarzenia B wynosi więc:

[14]

Zapis wyrażenia w formacie TeX-a:

P(B)=\frac{\overline{\overline{B}}}{\overline{\overline{\Omega}}}=\frac{12}{20}=\frac{3}{5}=60\%

Prawdopodobieństwo wylosowania liczb, których suma jest większa od dziesięciu jest równe 50%, a prawdopodobieństwo, że pierwsze z wylosowanych liczb będzie nieparzysta jest równe 60%.

Propozycje książek