Rozwiązywanie układów równań za pomocą wzorów Cramera

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 8306 razy

Czas obczaić kolejną dość ciekawą metodę rozwiązywania układów równań liniowych. Tą metodą są wzory Cramera, odkryte przez szwajcarskiego matematyka Gabriela Cramera.

Wzory te wykorzystują wyznaczniki macierzy kwadratowej spreparowanej z współczynników stojących przy niewiadomych oraz z wyrazów wolnych. Ogólny wzór wyznaczający i-tą niewiadomą w układzie równań przybiera postać następującą:

[1]

Zapis wyrażenia w formacie TeX-a:

x_i=\cfrac{W_i}{W_g}

gdzie:

x_i - i-ta niewiadoma
W_i - współczynnik macierzy utworzonej dla i-tej niewiadomej
W_g - współczynnik macierzy utworzonej z współczynników stojących przy niewiadomej

Zanim napiszę jak tworzone są macierze, poniżej zamieszczam postać, do której należy doprowadzić układ równań, aby możliwe było prawidłowe utworzenie takiej macierzy.

[2]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} a_{1,1}\cdot x_{1}+a_{2,1}\cdot x_{2}+\cdots+a_{n,1}\cdot x_{n}=b_{1} \\ a_{1,2}\cdot x_{1}+a_{2,2}\cdot x_{2}+\cdots+a_{n,2}\cdot x_{n}=b_{2} \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vdots \\ a_{1,n}\cdot x_{1}+a_{2,n}\cdot x_{2}+\cdots+a_{n,n}\cdot x_{n}=b_{n}\end{cases}

Macierz wyznacznika głównego W_g będzie więc przyjmowała następującą postać:

Macierz wyznacznika głównego potrzebna do rozwiązania układu równań metodą Cramera

[3]

Zapis wyrażenia w formacie TeX-a:

W_{g}=\begin{vmatrix}{a_{1,1}} && a_{2,1} && \cdots && a_{n,1} \\ a_{1,2} && a_{2,2} && \cdots && a_{n,2} \\ \vdots && \vdots && \vdots && \vdots \\ a_{1,n} && a_{2,n} && \cdots && a_{n,n}\end{vmatrix}

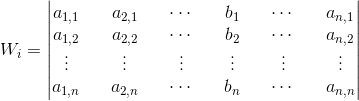
Macierz wyznacznika W_i jest podobna do macierzy głównego wyznacznika W_g z tą tylko różnicą, że i-tą kolumnę zastępuje kolumna wyrazów wolnych w następujący sposób:

Wzórn i-ty wyznacznik układu równań, niezbędny do obliczenia metodą Cramera

[4]

Zapis wyrażenia w formacie TeX-a:

W_{i}=\begin{vmatrix} a_{1,1} && a_{2,1} && \cdots && b_{1} && \cdots && a_{n,1} \\ a_{1,2} && a_{2,2} && \cdots && b_{2} && \cdots && a_{n,2} \\ \vdots && \vdots && \vdots && \vdots && \vdots && \vdots \\ a_{1,n} && a_{2,n} && \cdots && b_{n} && \cdots && a_{n,n}\end{vmatrix}

gdzie kolumna z wyrazami wolnymi: b₁, b₂, ..., b_n jest wstawiana za i-tą kolumnę macierzy wyznacznika głównego W_g.

Ogólny wzór na wyznacznik macierzy dowolnych rozmiarów, ma następującą postać:

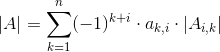Ogólny wzór na wyznacznik macierzy dowolnych rozmiarów metodą Laplece'a

[5]

Zapis wyrażenia w formacie TeX-a:

|A|=\sum_{k=1}^{n}(-1)^{k+i}\cdot a_{k,i}\cdot \left|A_{i,k}\right|

W dziale Matematyka → Macierze → Wyznacznik macierzy opisane zostało dokładnie zastosowanie wzoru [5], w celu więc zapoznania się z jego zastosowaniem odsyłam was do tamtego miejsca. Ja jedynie przytoczę tutaj jeszcze dwa wzory, pierwszy na wyznacznik macierzy o rozmiarach 2 x 2:

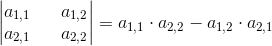Przykład obliczania wyznacznika macierzy 2x2

[6]

Zapis wyrażenia w formacie TeX-a:

\begin{vmatrix} a_{1,1} && a_{1,2} \\ a_{2,1} && a_{2,2} \end{vmatrix}=a_{1,1}\cdot a_{2,2}-a_{1,2}\cdot a_{2,1}

oraz dla macierzy 3 x 3:

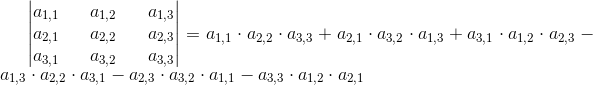Przykład obliczania wyznacznika macierzy 3x3

[7]

Zapis wyrażenia w formacie TeX-a:

\begin{vmatrix}a_{1,1} && a_{1,2} && a_{1,3} \\ a_{2,1} && a_{2,2} && a_{2,3} \\ a_{3,1} && a_{3,2} && a_{3,3}\end{vmatrix}=a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}-a_{2,3}\cdot a_{3,2}\cdot a_{1,1}-a_{3,3}\cdot a_{1,2}\cdot a_{2,1}

Zadanie 1

Rozwiązać układ równań z dwiema niewiadomymi: