Odbicia lustrzane
Stronę tą wyświetlono już: 8335 razy
O odbiciach lustrzanych a w zasadzie o macierzy odbicia lustrzanego i sposobach wszelakich jej pozyskiwania pisałem na stronie Matematyka → Macierze → Macierz odbicia lustrzanego, jeżeli więc kogoś z Was interesuje zgłębienie tego tematu, to odsyłam Was właśnie tam, albowiem temat jest dość obszerny i treściwy więc nie chcę dwa razy tego samego powtarzać, zwłaszcza, że nie miałoby to większego sensu. Z tego też względu ograniczę się do omówienia tworzenia macierzy i jej zastosowania w najprostszy z możliwych sposobów.
Odbicia lustrzane w układach 2W
Macierz odbicia lustrzanego w układzie 2W przyjmuje następującą postać:
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1977.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
gdzie kąt α stanowi kąt ustawienia prostej, względem której odbicie się odbywa. Kąt ten jest kątem skierowanym w kierunku od osi x przeciwnie do ruchu wskazówek zegara. Po wyliczeniu macierzy odbicia lustrzanego dowolną liczbę punktów można odbić mnożąc je przez ową macierz.
Wyprowadzenie wzoru na macierz odbicia lustrzanego znajduje się we wzorze [3] z strony Matematyka → Macierze → Macierz odbicia lustrzanego.
Możliwe jest również utworzenie macierzy odbicia lustrzanego za pomocą wektora kierunkowego. Nie będę jednak omawiał tutaj tego zagadnienia, gdyż zostało ono już omówione na wcześniej wspomnianej przeze mnie stronie a sposób wykorzystania tak stworzonej macierzy wygląda tak samo jak w wzorze [1]. Na rysunku 1 zamieszczam animację pokazującą efekt działania macierzy lustrzanego odbicia przykładowej figury płaskiej.
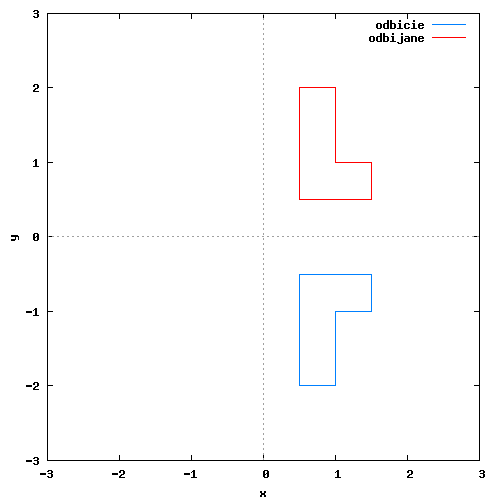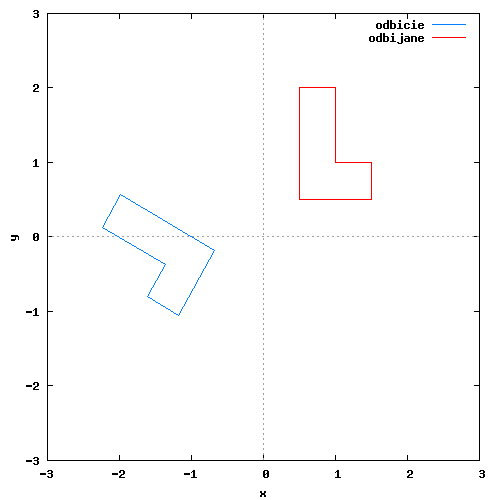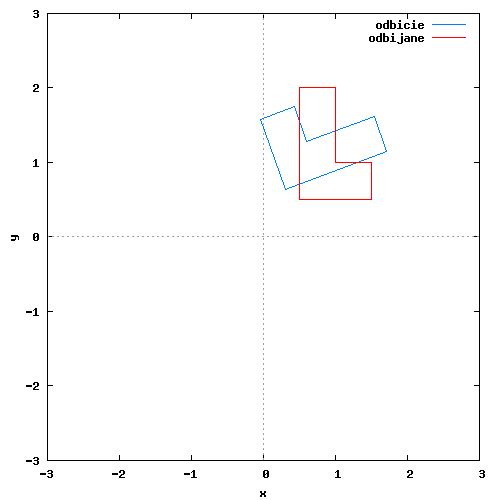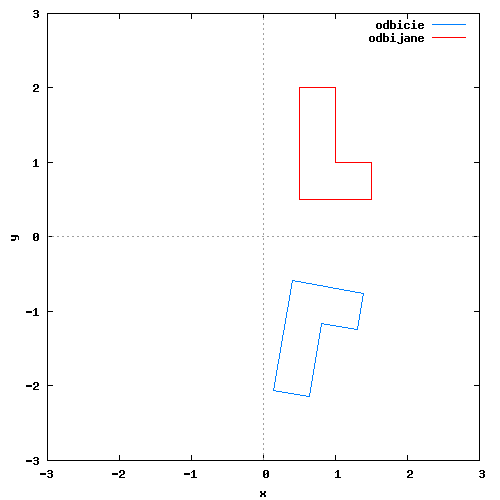
Klatki animacji wygenerowane przez program wxMaxima za pomocą następującego kodu:
Animacja poskładana w programie Gimp
Odbicia lustrzane w 3W
Najłatwiej jest utworzyć macierz odbicia lustrzanego znając wektor Vn prostopadły do płaszczyzny odbicia (zwany również wektorem normalnym płaszczyzny odbicia). Najpierw trzeba utworzyć wersor n tego wektora:
Teraz, dysponując wersorem n można obliczyć macierz odbicia lustrzanego za pomocą następującego wzoru, którego omówienie wyprowadzenia znajdziesz na wykładzie dostępnym na youtube.
gdzie:
- I - macierz jednostkowa, która ma na głównej przekątnej same jedynki, a reszta jej elementów przyjmuje wartość zerową;
- nT - transpozycja wektora, który traktujemy jak zwykłą macierz
Użycie macierzy odbicia lustrzanego w przestrzeni 3W jest takie samo jak w przestrzeni 2W co sprowadza się do następującego wzoru:
Na rysunku 2 zamieszczam animację przykładowego odbicia lustrzanego płaszczyzną obracającą się wokół osi Z.
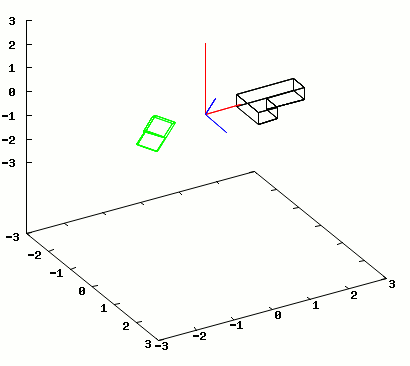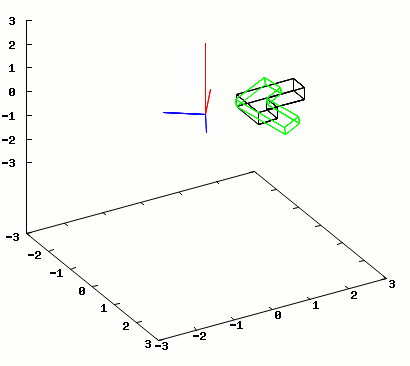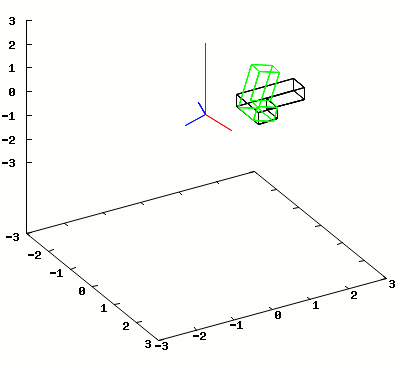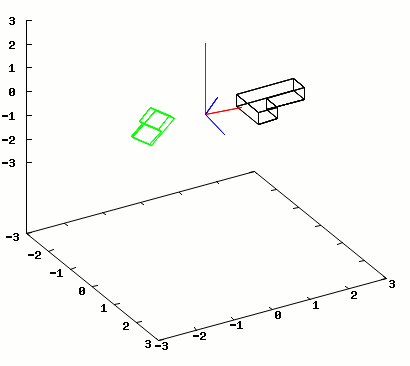
Klatki animacji wygenerowane przez program wxMaxima
Animacja poskładana w programie Gimp

![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1978.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1979.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_1944.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1980.gif)