Algorytm aproksymujący podane na wejście punkty metodą najmniejszych kwadratów

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 10100 razy

Opis matematyczny aproksymacji metodą najmniejszych kwadratów.

Niechaj istnieje taki zbiór punktów P₁, P₂, ..., P_m, dla których szukana jest funkcja w postaci wielomianu n-tego stopnia, gdzie n ≤ m-1. Punkty P₁, P₂, ..., P_m można zapisać w następującej postaci:

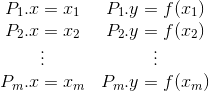
$begin{matrix}P_1.x = x_1 & P_1.y=f(x_1)\ P_2.x = x_2 & P_2.y=f(x_2)\ vdots & vdots\ P_m.x = x_m & P_m.y=f(x_m)end{matrix}$

[1]

sam zaś wielomian funkcji aproksymującej zadane punkty, będzie wyglądał w następujący sposób:

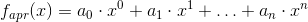
$f_{apr}(x)=a_0cdot x^0+a_1cdot x^1+hdots+a_ncdot x^n$

[2]

co z kolei można w prostszy sposób zapisać:

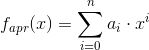
$f_{apr}(x)=sum_{i=0}^{n}a_icdot x^i$

[3]

Zaprawdę powiadam wam, że można wyznaczyć współczynniki a₀, a₁, ..., a_n wielomianu f_apr(x) układając następującą macierz:

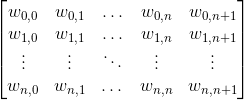
$begin{bmatrix}w_{0,0} & w_{0,1} & hdots & w_{0, n} & w_{0, n+1}\ w_{1,0} & w_{1,1} & hdots & w_{1, n} & w_{1, n+1} \ vdots & vdots & ddots & vdots & vdots \ w_{n, 0} & w_{n, 1} & dots & w_{n, n} & w_{n, n+1} end{bmatrix}$

[4]

gdzie współczynniki kolumn od 0 do n przyjmują wartości według następującego wzoru:

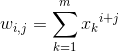
$w_{i, j}=sum_{k=1}^{m}{x_k}^{i+j}$

[5]

dla ostatniej kolumny zaś, wartości współczynników obliczyć z wzoru:

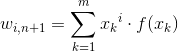
$w_{i, n+1}=sum_{k=1}^{m}{x_k}^{i}cdot f(x_k)$

[6]

Po wyliczeniu współczynników macierzy, należy niezwłocznie przejść do jej rozwiązania np. metodą Gaussa lub metodą Gaussa-Jordana.

Przykład rozwiązania

Niechaj podane będą następujące punkty: {1; 6}; {2; 8}; {4; 4}; {6; 2}; {8; 0}; {10; 2}. Wyznaczyć wielomian 2-giego stopnia aproksymujący te punkty.

Nie będzie wielkim rozwiązaniem tajemnicy, gdy stwierdzę, że konieczne jest utworzenie macierzy o rozmiarach n×n+1. Dla świętego spokoju rozpiszę tą macierz poniżej:

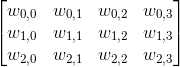
$begin{bmatrix}w_{0,0} & w_{0,1} & w_{0,2} & w_{0,3}\ w_{1,0} & w_{1,1} & w_{1,2} & w_{1,3}\ w_{2,0} & w_{2,1} & w_{2,2} & w_{2,3}end{bmatrix}$

[7]

Wyznaczenie współczynników o indeksach kolumn od 0 do 2 (czyli do n):

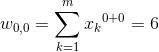
$w_{0,0}=sum_{k=1}^{m}{x_k}^{0+0}=6$

[8]

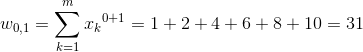
$w_{0,1}=sum_{k=1}^{m}{x_k}^{0+1}=1+2+4+6+8+10=31$

[9]

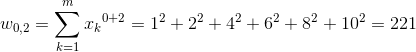
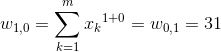
$w_{0,2}=sum_{k=1}^{m}{x_k}^{0+2}=1^2+2^2+4^2+6^2+8^2+10^2=221$

[10]

$w_{1,0}=sum_{k=1}^{m}{x_k}^{1+0}=w_{0,1}=31$

[11]

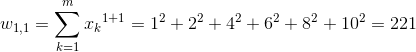
$w_{1,1}=sum_{k=1}^{m}{x_k}^{1+1}=1^2+2^2+4^2+6^2+8^2+10^2=221$

[12]

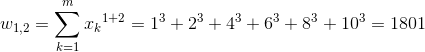
$w_{1,2}=sum_{k=1}^{m}{x_k}^{1+2}=1^3+2^3+4^3+6^3+8^3+10^3=1801$

[13]

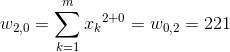
$w_{2,0}=sum_{k=1}^{m}{x_k}^{2+0}=w_{0,2}=221$

[14]

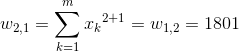
$w_{2,1}=sum_{k=1}^{m}{x_k}^{2+1}=w_{1,2}=1801$

[15]

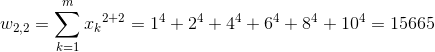
$w_{2,2}=sum_{k=1}^{m}{x_k}^{2+2}=1^4+2^4+4^4+6^4+8^4+10^4=15665$

[16]

Współczynniki ostatniej kolumny macierzy:

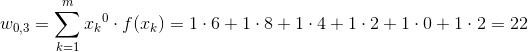
$w_{0,3}=sum_{k=1}^{m}{x_k}^{0}cdot f(x_k)=1cdot 6+1cdot 8 +1cdot 4+1cdot 2+1cdot 0+1cdot 2=22$

[17]

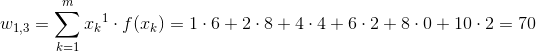
$w_{1,3}=sum_{k=1}^{m}{x_k}^{1}cdot f(x_k)=1cdot 6+2cdot 8 +4cdot 4+6cdot 2+8cdot 0+10cdot 2=70$

[18]

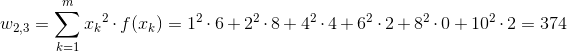
$w_{2,3}=sum_{k=1}^{m}{x_k}^{2}cdot f(x_k)=1^2cdot 6+2^2cdot 8 +4^2cdot 4+6^2cdot 2+8^2cdot 0+10^2cdot 2=374$

[19]

Najwyższy czas poskładać do kupy macierz:

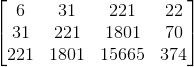
$begin{bmatrix}6 & 31 & 221 & 22\ 31 & 221 & 1801 & 70\ 221 & 1801 & 15665 & 374end{bmatrix}$

[20]

Nie będę tutaj rozwiązywał tej macierzy, powiem tylko, że jej rozwiązanie daje w wyniku następujące wartości współczynników szukanego wielomianu:

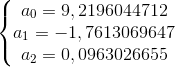
$left{ begin{matrix}a_0=9,2196044712\ a_1=-1,7613069647\ a_2=0,0963026655end{matrix}} right$

[21]

Funkcja f_apr(x)=a₀·x⁰+a₁·x¹+a₂·x²=9,2196044712-1,7613069647·x+0,0963026655·x² nie należy do najpiękniejszych, ale jak wynika z poniższego wykresu, działa ona bez zarzutu.

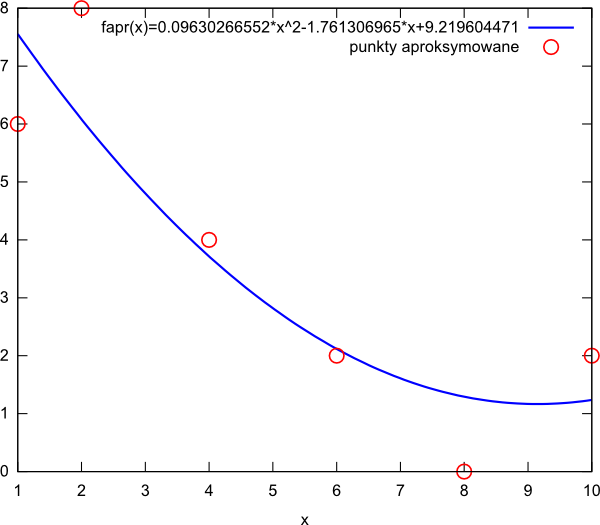
wykres aproksymacji — Rys. 1
Wykres aproksymacji punktów metodą najmniejszych kwadratów.

Wykres wygenerowany został w programie wxMaxima za pomocą następującego kodu:

plot2d([9.219604471*x^0-1.761306965*x^1+0.09630266552*x^2,[discrete,[[1, 6],[2, 8],[4, 4],[6, 2],[8, 0],[10, 2]]]],[x,1,10],[style,line,points],[gnuplot_term, "svg size 600,500"], [gnuplot_out_file, "C:\\aproksymacja.svg"],[legend,"fapr(x)=0.09630266552*x^2-1.761306965*x+9.219604471","punkty aproksymowane"]);

I edytowany w programie Inkscape

A na co to komu?

Stosuje się do uzyskania wzoru w postaci prostej funkcji wielomianowej punktów uzyskanych w wyniku przeprowadzanych pomiarów.

Program Aproksymator.exe

Pewnego dnia obudziłem się z przemożną chęcią napisania programu, który po podaniu odpowiednich danych na wejście wypluje mi na powierzchnię ekranu funkcję aproksymującą zadane punkty wielomianem stopnia, który ja podałem. Toteż i zakasałem rękawy i zrobiłem taki właśnie mały programik o dźwięcznej nazwie Aproksymator.exe.

Pragnę nadmienić, że program ten rozwiązanie zapisuje do pliku tekstowego aproksymacja.txt, gdzie w perfidny (żeby nie powiedzieć, że przebiegły) sposób program zapisuje dane wejściowe, funkcję aporoksymującą oraz (jakby tego było mało) kod niezbędny do wygenerowania wykresu punktów i funkcji aproksymującej w programie wxMaxima.

Przykład, rozwiązania wygenerowanego przez mój program rozwiązania dla wcześniej rozwiązywanego zadania z najdzikszą wręcz rozkoszą zamieszczam poniżej:

Oto rozwiązanie aproksymacji wielomianiem 2 stopnia następujących punktów: P1x= 1 P1y= 6 P2x= 2 P2y= 8 P3x= 4 P3y= 4 P4x= 6 P4y= 2 P5x= 8 P5y= 0 P6x= 10 P6y= 2 Funkcja aproksymujaca zadane punkty przyjmuje postac nastepujaca: fapr(x)=9.219604471*x^0-1.761306965*x^1+0.09630266552*x^2 Wykres w WxMaximie: plot2d([9.219604471*x^0-1.761306965*x^1+0.09630266552*x^2,[discrete,[[1, 6],[2, 8],[4, 4],[6, 2],[8, 0],[10, 2]]]],[x,1,10],[style,line,points])

Poniżej krótki filmik pokazujący działanie programu.

Załączniki:

Program Aproksymator do aproksymacji punktów metodą najmniejszych kwadratów