Wyznaczanie punktów zbieżności i podziałki zbiegu w perspektywie dwuzbieżnej
Stronę tą wyświetlono już: 9002 razy
Na poprzedniej stronie dotyczącej kreślenia obiektów w perspektywie dwuzbieżnej położenie punktów zbieżności określić można było znajdując położenie poszczególnych punktów, na które składały się krawędzie obiektu rysowanego w perspektywie dwuzbieżnej. Tym razem postaram się przybliżyć sposób pozyskiwania punktu zbiegu w bardziej ogólny sposób dla zbiorów prostych, które nie leżą w płaszczyźnie równoległej do płaszczyzny obserwacji, a które są względem siebie równoległe.
Wyznaczanie punktów zbiegu linii równoległych
Jeżeli mamy wyszczególnioną pewnego rodzaju "rodzinę" odcinków, o których wiadomo, że są one względem siebie równoległe, to o ile te odcinki, nie leżą w płaszczyznach równoległych do płaszczyzny obserwacji, to takie odcinki w perspektywie leżą na liniach przechodzących przez pewien punkt zbiegu Z.
Dla lepszego zrozumienia stwórzmy takie oto dwa rzuty prostopadłe trzech odcinków a, b i c, które są względem siebie równoległe a jednocześnie nie leżą w płaszczyznach równoległych do płaszczyzny patrzenia. Jak widać na rysunku 1 wszystkie trzy odcinki nie leżą na jednej płaszczyźnie, a ich perspektywistyczny rzut na płaszczyznę obserwacji daje w wyniku dość ciekawe rezultaty.

Opis oznaczeń
- a, b, c - rzuty prostopadłe linii równoległych;
- ap, bp, cp - linie a, b i c w rzucie perspektywistycznym na płaszczyznę patrzenia
- O - punkt patrzenia;
- Oτ - prostopadły rzut punktu patrzenia O na płaszczyznę patrzenia;
- Z - punkt zbieżności linii ap, bp i cp
- h - horyzont.
Z powyższej ilustracji wynika niezbicie, że niezależnie od tego, czy dane linie leżą, czy też nie leżą w jednej płaszczyźnie, mają one w perspektywie punkt zbieżności Z. Punkt zbieżności Z jest ściśle powiązany z kątem α zawartym pomiędzy prostymi a, b i c a płaszczyzną patrzenia. Kąt ten został oznaczony na poniższej ilustrzcji.
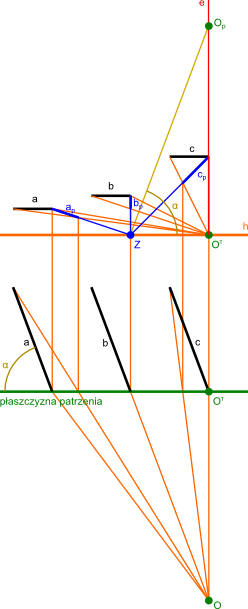
Opis oznaczeń
- a, b, c - rzuty prostopadłe linii równoległych;
- ap, bp, cp - linie a, b i c w rzucie perspektywistycznym na płaszczyznę patrzenia
- O - punkt patrzenia;
- Oτ - prostopadły rzut punktu patrzenia O na płaszczyznę patrzenia;
- Z - punkt zbieżności linii ap, bp i cp
- h - horyzont.
- α - kąt zawart pomiędzy dolnym rzutem prostopadłym prostych a, b i c a płaszczyzną patrzenia;
- e - linia pionu
- Op - punkt patrzenia na linii poziomu e znajdująca się w odległości równej promieniowi patrzenia δ od punktu Oτ.
Z rysunku 2 można wywnioskować, że odnalezienie punktu zbiegu Z jest możliwe poprzez zaznaczenie na prostej poziomu e w odległości równej promieniowi patrzenia δ od punktu Oτ punktu patrzenia Op. Z tego punktu pod kątem α względem linii horyzontu h należy poprowadzić prostą, której punkt przecięcia się z linią horyzontu h wyznacza pukt zbiegu Z.
Podziałki zbiegu
Bardzo często zdarza się, że punkt zbiegu Z danej grupy linii czy też raczej odcinków znajduje się daleko. W takim przypadku, gdy perspektywa kreślona jest na arkuszu o określonych wymiarach nie jest możliwe posłużenie się w sposób bezpośredni punktem zbiegu Z, gdyż ten wybiega daleko poza obszar rysowania. Na szczęście istnieje metoda podziałek zbiegu.

Opis oznaczeń
- δ - promień patrzenia;
- Oτ - rzut punktu oka O na płaszczyznę obserwacji;
- Pp - przykładowy punkt w perspektywie;
- Z - główny punkt zbiegu;
- Z1/2 - punkt zbiegu dla podziałki równej
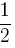 ;
; - Z1/4 - punkt zbiegu dla podziałki równej
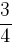 ;
; - e - główna pozioma podziałka;
- e1/2 - oś podziałki stanowiącej
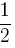 wartości podziałki głównej e;
wartości podziałki głównej e; - e1/4 - oś podziałki stanowiącej
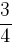 wartości podziałki głównej e;
wartości podziałki głównej e; - Op - punkt patrzenia dla głównego punktu zbiegu Z;
- Op1/2 - punkt patrzenia dla punktu zbiegu Z1/2;
- Op1/4 - punkt patrzenia dla punktu zbiegu Z1/4
Podziałki zbiegu widoczne na rysunku 3 mają wartości odnoszące się do podziałki głównej w pewnym stosunku. Stosunek ten jest ściśle związany z stosunkiem odległości dzielącej punkt Oτ od punktu Op1/4 do promienia patrzenia δ. Jedna działka skali głównej e jest równa w tym przypadku 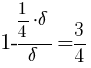 . Na przykładzie punktu leżącego w perspektywie Pp widać, że linia łącząca punkt zbiegu Z z punktem Pp przecina oś e, e1/4 i e1/2 w tej samej odległości na ich własnych skalach. W ten właśnie sposób można znaleźć linię zbiegu bez znajomości punktu zbiegu Z.
. Na przykładzie punktu leżącego w perspektywie Pp widać, że linia łącząca punkt zbiegu Z z punktem Pp przecina oś e, e1/4 i e1/2 w tej samej odległości na ich własnych skalach. W ten właśnie sposób można znaleźć linię zbiegu bez znajomości punktu zbiegu Z.
Metoda równoległego przesunięcia
Teraz omówię inną znacznie ciekawszą moim zdaniem metodę znajdowania linii zbiegu. Jest ona o tyle ciekawsza, że nie jest konieczne kreślenie podziałek zbiegu tak jak było to omawiane wcześniej. Okazuje się, że wystarczy dany punkt w perspektywie Pp połączyć z punktem Oτ a odległość dzielącą owe punkty pomnożyć przez skalę odpowiadającą danemu punktowi zbiegu (mp. dla Z1/4 skala wynosi 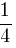 . Odnaleziony punkt Pp1/4 połączyć z punktem zbiegu Z1/4 a otrzymaną prostą przenieść równolegle tak, aby przechodziła ona przez punkt perspektywy Pp tym samym wyznaczając prostą zbiegu dla prostej przechodzącej przez tenże punkt.
. Odnaleziony punkt Pp1/4 połączyć z punktem zbiegu Z1/4 a otrzymaną prostą przenieść równolegle tak, aby przechodziła ona przez punkt perspektywy Pp tym samym wyznaczając prostą zbiegu dla prostej przechodzącej przez tenże punkt.
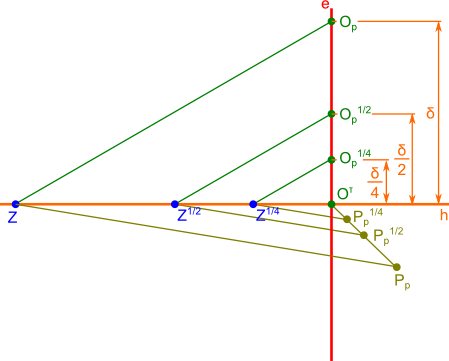
Opis oznaczeń
- δ - promień patrzenia;
- Oτ - rzut punktu oka O na płaszczyznę obserwacji;
- Pp - przykładowy punkt w perspektywie;
- Pp1/2 - punkt Pp w skali
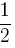 ;
; - Pp1/4 - punkt Pp w skali
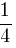 ;
; - Z - główny punkt zbiegu;
- Z1/2 - punkt zbiegu dla podziałki równej
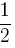 ;
; - Z1/4 - punkt zbiegu dla podziałki równej
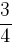 ;
; - e - oś poziomu;
- Op - punkt patrzenia dla głównego punktu zbiegu Z;
- Op1/2 - punkt patrzenia dla punktu zbiegu Z1/2;
- Op1/4 - punkt patrzenia dla punktu zbiegu Z1/4"
