Punkty mierzenia i punkty częściowego mierzenia.
Stronę tą wyświetlono już: 5227 razy
Nadszedł czas opowiedzieć co nieco o bardzo ciekawym sposobie odnajdowania punktów na linii zbiegu. W tym celu konieczne będzie wprowadzenie pojęcia punktów mierzenia M oraz częściowego mierzenia, które umożliwią odmierzanie konkretnych rzeczywistych długości danego odcinka biegnącego pod zadanym kątem α względem płaszczyzny patrzenia.
Znajdowanie punktów mierzenia oraz ich zastosowanie.
Rozpatrzmy następujący przypadek: dany jest punkt P, który znajduje się poniżej linii horyzontu h w odległości 4 cm i 6 cm od linii poziomu e oraz 2 cm za płaszczyzną patrzenia. Przez tenże punkt P przechodzi prosta a pod kątem α=60° względem płaszczyzny patrzenia. Wyznaczyć w perspektywie odcinek zaczynający się w punkcie P o rzeczywistej długości 10 cm. Promień patrzenia δ=5 cm.
Na podstawie powyższego opisu możliwe jest sporządzenie rysunku 1, gdzie narysowana została linia horyzontu h, linia poziomu e oraz położenie punktu P w rzucie prostopadłym na płaszczyznę równoległą do płaszczyzny patrzenia.
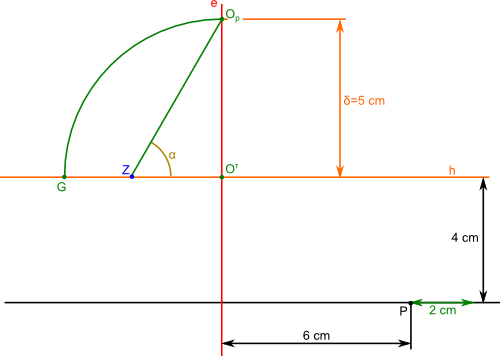
Opis oznaczeń:
- P - punkt w rzucie prostopadłym na rzutnię równoległą do płaszczyzny patrzenia;
- Op - punkt patrzenia niezbędny do wyznaczenia punktu zbiegu Z;
- Z - punkt zbiegu dla kąta α=60°;
- Oτ - rzut punktu obserwacji O;
- G - punkt mierzenia głębi, który w tym przypadku posłuży do wyznaczenia położenia punktu P w perspektywie;
- δ - promień patrzenia.
Wszystkie elementy z rysunku 1 powinny być już dobrze znane z wcześniejszych stron, jak również sposób wyznaczenia punktu P w perspektywie. Na rysunku 2 jest już gotowy wyznaczony punkt Pp znajdujący się w perspektywie oraz coś czego jeszcze nie było, czyli wyznaczony został punkt mierzenia M. Ten punkt wyznacza przecięcie się linii horyzontu h z łukiem zakreślonym z punktu Z rozwartością równą odległości dzielącej punkt zbiegu Z od punktu patrzenia Op.
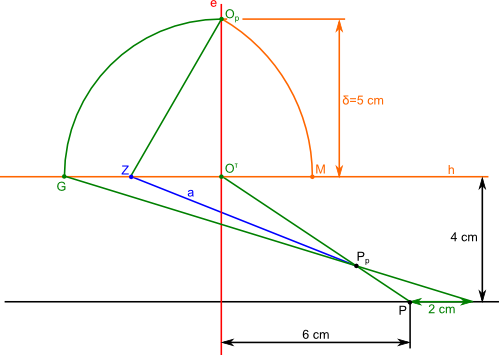
Opis oznaczeń:
- P - punkt w rzucie prostopadłym na rzutnię równoległą do płaszczyzny patrzenia;
- Op - punkt patrzenia niezbędny do wyznaczenia punktu zbiegu Z;
- Z - punkt zbiegu dla kąta α=60°;
- Oτ - rzut punktu obserwacji O;
- G - punkt mierzenia głębi, który w tym przypadku posłuży do wyznaczenia położenia punktu P w perspektywie;
- δ - promień patrzenia;
- M - punkt mierzenia.
Odmierzenie żądanej odległości równej 10 cm jest możliwe poprzez znalezienie przecięcia się prostej równoległej do linii horyzontu h i przechodzącej przez punkt P z prostą przechodzącą przez punkt mierzenia M i punkt Pp. Od wspomnianego punktu przecięcia należy odmierzyć odległość 10 cm (jak z resztą uczyniłem to na poniższym rysunku) i uzyskany w ten sposób punkt połączyć z punktem mierzenia M. Tym przebiegłym skądinąd sposobem odnaleziony został punkt P2p stanowiący koniec szukanego odcinka.
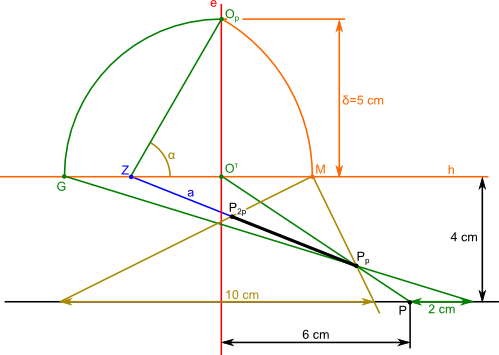
Opis oznaczeń:
- P - punkt w rzucie prostopadłym na rzutnię równoległą do płaszczyzny patrzenia;
- Op - punkt patrzenia niezbędny do wyznaczenia punktu zbiegu Z;
- Z - punkt zbiegu dla kąta α=60°;
- Oτ - rzut punktu obserwacji O;
- G - punkt mierzenia głębi, który w tym przypadku posłuży do wyznaczenia położenia punktu P w perspektywie;
- δ - promień patrzenia;
- M - punkt mierzenia.
- P - punkt w rzucie prostopadłym na rzutnię równoległą do płaszczyzny patrzenia;
- Op - punkt patrzenia niezbędny do wyznaczenia punktu zbiegu Z;
- Z - punkt zbiegu dla kąta α=60°;
- Oτ - rzut punktu obserwacji O;
- G - punkt mierzenia głębi, który w tym przypadku posłuży do wyznaczenia położenia punktu P w perspektywie;
- δ - promień patrzenia;
- M - punkt mierzenia;
- M1/2 - punkt częściowego mierzenia o skali
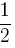 .
.
Punkty częściowego mierzenia
Niekiedy wygodniej jest używać tak zwanych punktów częściowego mierzenia, które zmieniają skalę wykorzystywanych do wyznaczenia danego odcinka na linii zbiegu odległości. Jest to istotne, ponieważ długości danych odcinków mogą wykraczać znacznie poza obszar rysowania, co uniemożliwia a co najmniej utrudnia wyznaczenie danego odcinka na linii zbiegu. Punkty częściowego mierzenia zmniejszają skalę tych odcinków, przez co umożliwiają znalezienie danego odcinka na linii zbiegu nawet, gdy punkt mierzenia lub odległość mierzona wykracza poza obszar rysunkowy.
Dla wcześniej rozważanego przykładu z punktem mierzenia M można zastosować z takim samym skutkiem punkt częściowego mierzenia M1/2, dla skali 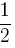 , która oznacza, że punkt ten znajduje się w
, która oznacza, że punkt ten znajduje się w 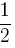 odległości dzielącej punkt zbiegu Z od punktu mierzenia M. Przez ten sam współczynnik należy przemnożyć odkładaną na linii przechodzącej przez punkt P i równoległą do linii horyzontu h odmierzaną odległość, czyli 10 cm. Jak widać na rysunku 4 połączenie uzyskanych w ten sposób punktów daje ten sam punkt Pp.
odległości dzielącej punkt zbiegu Z od punktu mierzenia M. Przez ten sam współczynnik należy przemnożyć odkładaną na linii przechodzącej przez punkt P i równoległą do linii horyzontu h odmierzaną odległość, czyli 10 cm. Jak widać na rysunku 4 połączenie uzyskanych w ten sposób punktów daje ten sam punkt Pp.
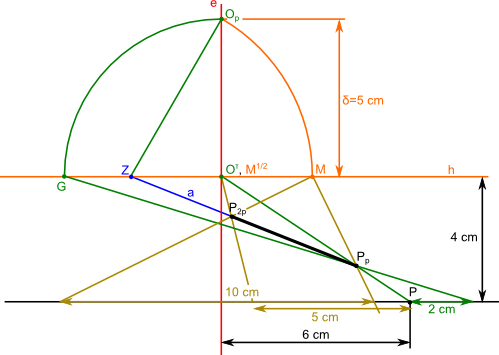
Opis oznaczeń:
