Ciągi geometryczne
Stronę tą wyświetlono już: 3419 razy
Podstawowe definicje ciągu geometrycznego
Ciąg liczbowy (an) jest ciągiem geometrycznym wtedy i tylko wtedy, gdy jest on co najmniej trójelementowy, a każdy z elementów tego ciągu począwszy od drugiego powstaje poprzez pomnożenie elementu poprzedniego przez stałą liczbę q nazywaną ilorazem ciągu.
Skończony ciąg (a1, a2, ..., an) jest ciągiem geometrycznym wtedy i tylko wtedy, gdy jest co najmniej trójelementowy, a każdy element począwszy od drugiego powstaje poprzez pomnożenie elementu poprzedniego przez stałą liczbę q nazywaną ilorazem ciągu.
Wzór na n-ty element ciągu geometrycznego
Wzór rekurencyjny:
Wzór bezpośredni:
Wzór na sumę n początkowych elementów ciągu geometrycznego
Gdy q = 1:
Gdy q ≠ 1:
Monotoniczność ciągu geometrycznego
Ciąg geometryczny jest rosnący:
- gdy q > 1 i a1 > 0;
- gdy q ∈ (0; 1) i a1 < 0
Ciąg geometryczny jest malejący:
- gdy q > 1 i a1 < 0;
- gdy q ∈ (0; 1) i a1 > 0
Ciąg geometryczny jest stały:
- gdy q = 1;
- gdy a1 = 0
Zbieżność ciągu geometrycznego
Gdy q = 1 lub a1 = 0, wtedy:
Gdy |q| < 1, wtedy:
Ciąg geometryczny jest naprzemienny gdy q < 0
Zależność elementów ciągu geometrycznego
Jeżeli dane są dwa elementy ciągu geometrycznego, których różnica indeksów jest podzielna przez dwa to:

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

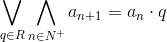
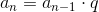
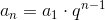
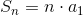
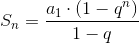
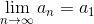
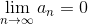
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2868.gif)