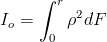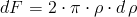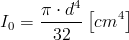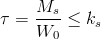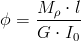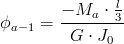Stronę tą wyświetlono już: 20957 razy

Wyznaczenie wzoru na biegunowy moment bezwładności pełnego przekroju kołowego

Biegunowy moment bezwładności liczy się w podobny sposób jak moment bezwładności względem danej osi, z tą tylko różnicą, że pole powierzchni elementarnej dF mnożone jest przez kwadrat odległości od środka obrotu. Dla przekroju kołowego można więc napisać następujący wzór:

[1]

Zapis wyrażenia w formacie TeX-a:

I_{o}=\int_0^r\rho ^2 dF

gdzie dF jest polem powierzchni, które z kolei dla kołowego przekroju jest równe:

[2]

Zapis wyrażenia w formacie TeX-a:

dF=2\cdot \pi\cdot \rho \cdot d\, \rho

Podstawiamy więc do wzoru [1] za dF wartość z wzoru [2] i przystępujemy do obliczenia odśrodkowego momentu bezwładności:

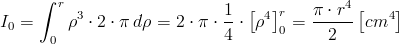[3]

Zapis wyrażenia w formacie TeX-a:

I_{0}=\int_0^r\rho ^3\cdot 2\cdot \pi\, d\rho=2\cdot \pi\cdot \frac{1}{4}\cdot \left[\rho^4\right]_0^r=\frac{\pi\cdot r^4}{2}\left[cm^4\right]

Ponieważ przy obliczeniach wytrzymałościowych częściej używa się średnicy d niż promienia r zatem wzór [4] można przekształcić do następującej postaci:

[4]

Zapis wyrażenia w formacie TeX-a:

I_{0}=\frac{\pi \cdot d^4}{32}\left[cm^4\right]

Przy okazji można też obliczyć wskaźnik wytrzymałości na skręcanie W₀:

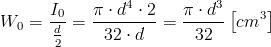[5]

Zapis wyrażenia w formacie TeX-a:

W_{0}=\frac{I_{0}}{\frac{d}{2}}=\frac{\pi\cdot d^4\cdot 2}{32\cdot d}=\frac{\pi\cdot d^3}{32}\left[cm^3\right]

Dla przekrojów drążonych wzór na biegunowy moment bezwładności I₀ można wyprowadzić korzystając z wzoru [4] obliczając różnicę momentu bezwładności okręgu o średnicy D i okręgu o średnicy d w następujący sposób:

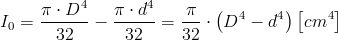[6]

Zapis wyrażenia w formacie TeX-a:

I_{0}=\frac{\pi\cdot D^4}{32}-\frac{\pi\cdot d^4}{32}=\frac{\pi}{32}\cdot \left(D^4-d^4\right)\left[cm^4\right]

Wskaźnik wytrzymałości na skręcanie:

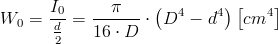[7]

Zapis wyrażenia w formacie TeX-a:

W_{0}=\frac{I_{0}}{\frac{d}{2}}=\frac{\pi}{16\cdot D}\cdot \left(D^4-d^4\right)\left[cm^4\right]

Wyznaczanie naprężenia stycznego (skręcającego)

Pod wpływem momentu skręcającego w danym przekroju powstają naprężenia styczne, których wartość nie powinna przekraczać granicznej wartości naprężenia stycznego k_s zależnej od materiału, z jakiego wykonany został rozpatrywany element. Naprężenie styczne można obliczyć korzystając z następującego wzoru:

[8]

Zapis wyrażenia w formacie TeX-a:

\tau = \frac{M_{s}}{W_{0}}\leq k_s

Kąt skręcania pręta

Pod wpływem momentów skręcających następuje skręcenie przekroju o kąt, którego wartość można obliczyć ze wzoru:

[9]

Zapis wyrażenia w formacie TeX-a:

\phi = \frac{M_{\rho}\cdot l}{G\cdot I_0}

Zadanie 1

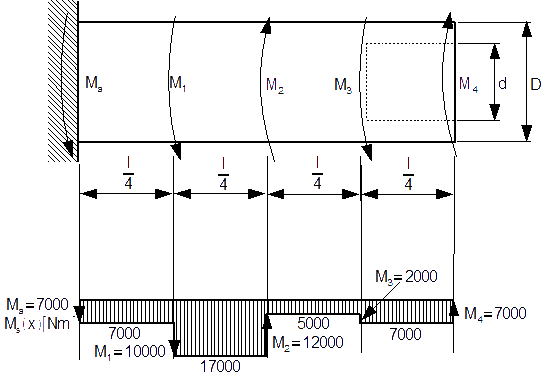
Dla stalowego wału z rysunku 2 należy obliczyć wartości naprężeń stycznych w każdym z czterech przekrojów.

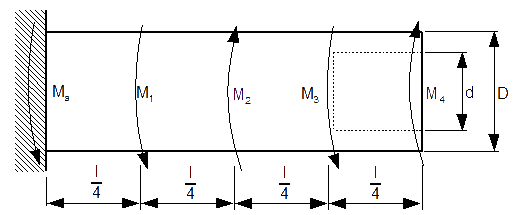
Dane:

Rozwiązanie:

Wskaźnik wytrzymałości na skręcania W_op dla przekroju pełnego:

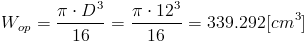[10]

Zapis wyrażenia w formacie TeX-a:

W_{op}=\frac{\pi\cdot D^3}{16}=\frac{\pi\cdot 12^3}{16}=339.292[cm^3]

Wskaźnik wytrzymałości na skręcania W_od dla przekroju drążonego:

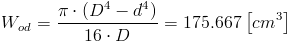[11]

Zapis wyrażenia w formacie TeX-a:

W_{od}=\frac{\pi\cdot \left(D^4-d^4\right)}{16\cdot D}=175.667\left[cm^3\right]

Wyznaczenie reakcji M_a:

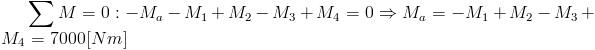[12]

Zapis wyrażenia w formacie TeX-a:

\sum M=0: -M_a-M_1+M_2-M_3+M_4 =0\Rightarrow M_{a}=-M_1+M_2-M_3+M_4=7000[Nm]

Obliczenia naprężeń stycznych w poszczególnych przekrojach belki:

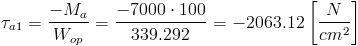[13]

Zapis wyrażenia w formacie TeX-a:

\tau_{a1}=\frac{-M_{a}}{W_{op}}=\frac{-7000\cdot 100}{339.292}=-2063.12\left[\frac{N}{cm^2}\right]

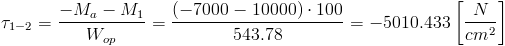[14]

Zapis wyrażenia w formacie TeX-a:

\tau _{1-2}=\frac{-M_{a}-M_{1}}{W_{op}}=\frac{(-7000-10000)\cdot 100}{543.78}=-5010.433\left[\frac{N}{cm^2}\right]

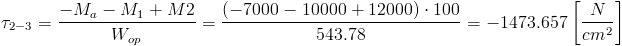[15]

Zapis wyrażenia w formacie TeX-a:

\tau_{2-3}=\frac{-M_{a}-M_{1}+M_{2}}{W_{op}}=\frac{(-7000-10000+12000)\cdot 100}{543.78}=-1473.657\left[\frac{N}{cm^2}\right]

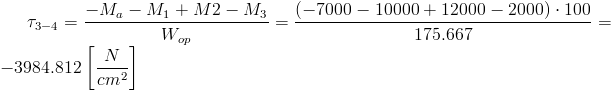[16]

Zapis wyrażenia w formacie TeX-a:

\tau _{3-4}=\frac{-M_{a}-M_{1}+M{2}-M_{3}}{W_{op}}=\frac{(-7000-10000+12000-2000)\cdot 100}{175.667}=-3984.812\left[\frac{N}{cm^2}\right]

Zadanie 2

Stalowy wał z rysunku 4 zrobiony ma zostać z materiału, którego maksymalne naprężenie skręcające k_s wynosi 3000 [N/cm²] wyznaczyć średnicę D taką aby wał mógł przenosić zadane obciążenie skręcające.

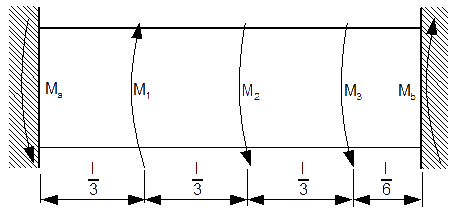
Dane:

Rozwiązanie:

Statyczne równanie równowagi:

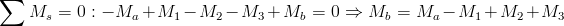[17]

Zapis wyrażenia w formacie TeX-a:

\sum M_s=0: -M_a+M_1-M_2-M_3+M_b=0\Rightarrow M_{b}=M_a-M_1+M_2+M_3

Ten wał jest statycznie niewyznaczalny, ale ponieważ utwierdzony jest on końcami więc suma wszystkich kątów skręcających musi być równa zero. W celu napisania dodatkowego równania należy dziabnąć wał na cztery przekroje i dla każdego z nich napisać równanie określające kąt skręcenia belki w danym przekroju. Po ułożeniu wszystkich równań, należy je zsumować i przyrównać do zera (warunek związany z utwierdzeniem sztywnym wału).

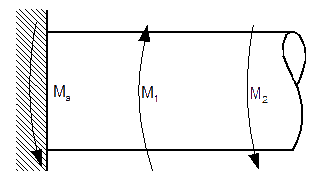
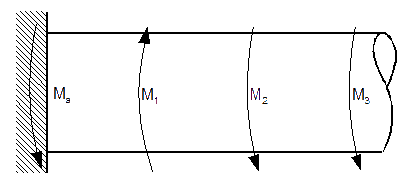
Przekroje

[18]

Zapis wyrażenia w formacie TeX-a:

\phi_{a-1}=\frac{-M_{a}\cdot \frac{l}{3}}{G\cdot J_0}

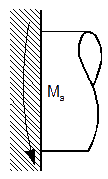
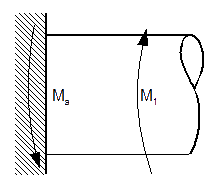
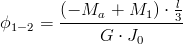[19]

Zapis wyrażenia w formacie TeX-a:

\phi_{1-2}=\frac{\left(-M_{a}+M_1\right)\cdot \frac{l}{3}}{G\cdot J_0}

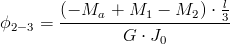[20]

Zapis wyrażenia w formacie TeX-a:

\phi_{1-2}=\frac{\left(-M_{a}+M_1-M_2\right)\cdot \frac{l}{3}}{G\cdot J_0}

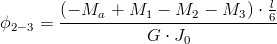[21]

Zapis wyrażenia w formacie TeX-a:

\phi_{2-3}=\frac{\left(-M_{a}+M_1-M_2-M_3\right)\cdot \frac{l}{6}}{G\cdot J_0}

Teraz należy zsumować równania z poszczególnych przekrojów:

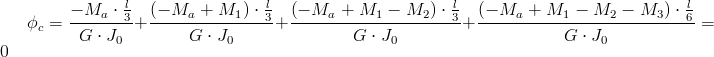[22]

Zapis wyrażenia w formacie TeX-a:

\phi_{c}=\frac{-M_{a}\cdot \frac{l}{3}}{G\cdot J_0}+\frac{\left(-M_{a}+M_1\right)\cdot \frac{l}{3}}{G\cdot J_0}+\frac{\left(-M_{a}+M_1-M_2\right)\cdot \frac{l}{3}}{G\cdot J_0}+\frac{\left(-M_{a}+M_1-M_2-M_3\right)\cdot \frac{l}{6}}{G\cdot J_0}=0

Po przekształceniu równania [22] otrzymujemy wzór na M_a:

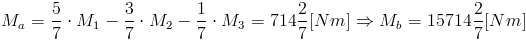[23]

Zapis wyrażenia w formacie TeX-a:

M_{a}=\frac{5}{7}\cdot M_1-\frac{3}{7}\cdot M_2-\frac{1}{7}\cdot M_3=714\frac{2}{7}[Nm]\Rightarrow M_{b}=15714\frac{2}{7}[Nm]

Do obliczeń średnicy D wału trzeba znaleźć wartość maksymalnego momentu skręcającego, w związku z czym należy wykonać wykres momentów skręcających. Licząc od prawej strony dla przedziału pierwszego moment skręcający powoduje tylko reakcja M_a, dla następnego M_a + M₁ itd. aż do ostatniego przedziału. W ten sposób tworzony jest wykres momentów skręcających.

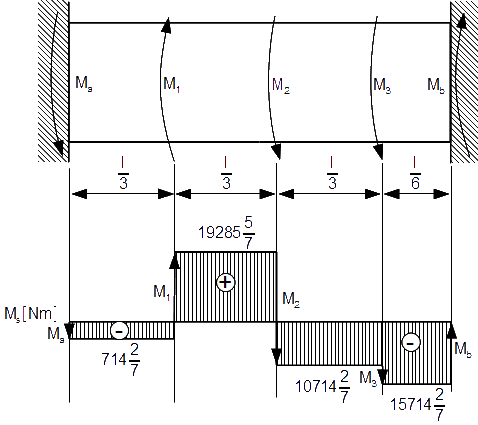
Skoro już wiadomo, ile wynosi maksymalny moment skręcający M_{s max} można już obliczyć minimalną średnicę wału, która będzie w stanie przenosić takie obciążenia wykorzystując w tym niecnym celu wzory [8] i [5]:

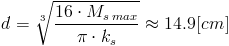[24]

Zapis wyrażenia w formacie TeX-a:

d=\sqrt[3]{\frac{16\cdot M_{s, max}}{\pi \cdot k_s}}\approx 14.9[cm]

Przy obliczeniach należy maksymalny moment skręcający Ms max zamienić z Nm na Ncm bo inaczej wyjdzie masło maślane.