Stronę tą wyświetlono już: 2047 razy

Dość ciekawym problemem, z którym czasami się stykam jest konieczność wyznaczenia wektora, który dzieli kąt pomiędzy dwoma innymi wektorami na dwie równe części. Z technicznego punktu widzenia można taki wektor wyznaczyć wyliczając kąt pomiędzy tymi wektorami lecz w tym konkretnym przypadku taka konieczność nie występuje. Dzieje się tak, albowiem wystarczy zapewnienie, że oba wektory V₁ i V₂ nie są wektorami zerowymi ani wektorami o przeciwnych zwrotach i tym samym kierunku. Gdy te dwa warunki są spełnione to wyznaczenie wektora siecznego V_s będzie wymagało jedynie wykorzystania następującego wzoru:

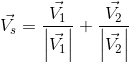[1]

Zapis wyrażenia w formacie TeX-a:

\vec{V_s}=\frac{\vec{V_1}}{\left|\vec{V_1}\right|}+\frac{\vec{V_2}}{\left|\vec{V_2}\right|}

Jak widać oba wektory zostały poddane normalizacji, czyli przeskalowaniu ich tak, aby wartość każdego z nich była równa 1 dzięki takiemu stanowi rzeczy interpretacja geometryczna dodawania dwóch wektorów o takiej samej długości pokazuje, że takie wektory tworzą w konstrukcyjnym dodawaniu romb a przekątna rombu zawsze dzieli kąt na dwie równe części.