Konstrukcja chwilowego środka obrotu

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 16553 razy

Konstrukcja chwilowego środka obrotu umożliwia obliczenie prędkości obranego punktu B pod warunkiem, że znana jest informacja o prędkości jednego z punktów A oraz kierunek prędkości punktu B. Punkt chwilowego środka obrotu można wyznaczyć poprzez poprowadzenie dwóch linii, pierwszej z punktu A prostopadłej do kierunku wektora jego ruchu oraz z punktu B również prostopadle do kierunku wektora prędkości. Punkt przecięcia tak poprowadzonych linii jest środkiem chwilowego obrotu.

Relacja chwilowej prędkości V_A, V_B, długości odcinka |AS| oraz |BS| jest następująca:

[1]

Zapis wyrażenia w formacie TeX-a:

\omega_s =\frac{V_{A}}{|AS|}=\frac{V_{B}}{|BS|}

Zadanie 1

Dwa suwaki połączone przegubowo za pośrednictwem cięgna o długości l poruszają się po prostopadłych do siebie suwnicach. Obliczyć prędkość V_B suwadła B zakładając, że prędkość V_A suwadła A, kąt α oraz długość l cięgna są dane.

Rysunek zastosowania konstrukcji chwilowego środka ciężkości — Rys. 2
Układ dwóch suwaków połączonych z sobą przegubowo za pomocą cięgna.

Dane:

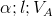
$alpha; l; V_{A}$

Rozwiązanie:

Stosując równanie [1] można wyznaczyć prędkość V_B w następujący sposób:

[2]

Zapis wyrażenia w formacie TeX-a:

V_{B}=V_{A}\cdot \frac{|BO|}{|AO|}=V_A\cdot \frac{l\cdot \sin\alpha}{l\cdot \cos\alpha}=V_{A}\cdot \tan\alpha

Zadanie 2

Obliczyć prędkość liniową punktu A okręgu toczącego się bez poślizgu po płaskiej poziomej powierzchni, którego prędkość liniowa V_S jest znana.

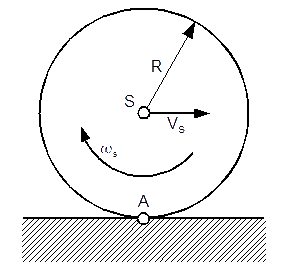
Rysunek do zadania 2 — Rys. 3
Ilustracja okręgu toczącego się bez poślizgu po płaskiej poziomej płaszczyźnie.

Dane:

R, V_S

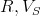
Rozwiązanie:

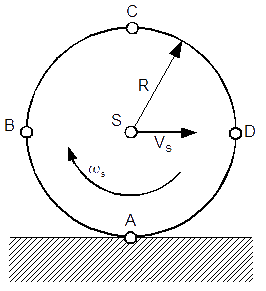
Na prędkość punktu A okręgu toczącego się bez poślizgu składają się dwa wektory prędkości: pierwszy to wektor prędkości środka okręgu V_S oraz drugi to wektor chwilowej prędkości punktu A wynikający z toczenia się bez poślizgu a więc z ruchu obrotowego tego okręgu. Dla lepszego zrozumienia na rysunku 4 naniesione zostały oba wektory prędkości działające na punkt A okręgu.

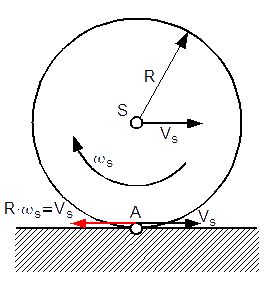
Wektor wypadkowy prędkości punktu A stycznego do płaszczyzny poziomej jest wektorem zerowym. Oczywiście prędkość tego punktu jest prędkością chwilową, co oznacza że punkt A jest punktem chwilowego środka obrotu i można go wykorzystać do obliczenia chwilowej prędkości dowolnego punktu okręgu.

Zadanie 3

Obliczyć prędkość liniową punktu B, C oraz D okręgu toczącego się bez poślizgu po płaskiej poziomej powierzchni, którego prędkość liniowa V_S jest znana.

Dane:

R, V_S

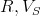
Rozwiązanie:

Tak jak w przypadku zadania 3 na prędkość każdego z wyznaczonych punktów składają się wektory: prędkości V_S środka okręgu i prędkości obwodowej, który jest równy wartości wektora V_S, lecz przyjmuje różny kierunek i zwrot zależny od położenia obranego punktu na obwodzie koła. Jak widać na rysunku 6 możliwe jest obliczenie wartości wektora prędkości bezwzględnej danego punktu okręgu poprzez dodanie wektorów V_S prędkości środka okręgu i prędkości obwodowej danego punktu okręgu.

Oczywiście możliwe jest rozwiązanie tego zadania z wykorzystaniem konstrukcji chwilowego środka obrotu, lecz w tym przypadku mija to się z celem, ponieważ wektory składowe są dane i ułożone w taki sposób, że ich wyznaczenie poprzez proste dodanie jest prostsze.

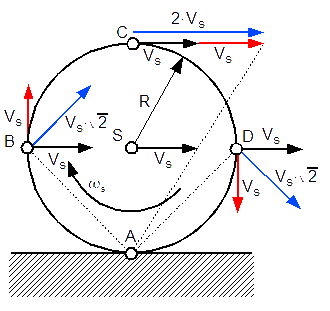
Rysunek do zadania 3 — Rys. 6
Wyznaczanie wektorów prędkości punktów B, C oraz D.

Zadanie 4

Obliczyć prędkość liniową środka V_S oraz prędkość kątową ω_S elementu tocznego znajdującego się pomiędzy liniałem poruszającym się z prędkością V₁ a podłożem poruszającym się z prędkością V₂. Średnica mniejszego koła elementu rocznego jest dwa razy mniejsza od średnicy koła dużego.

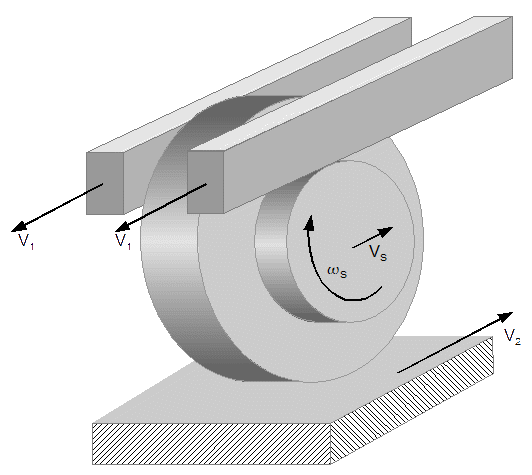
Rysunek do zadania 4 — Rys. 7
Układ do **zadania 4**.

Dane:

$V_1=10left[frac{m}{s}right]; V_2=40left[frac{m}{s}right];frac{r}{R}=2[-];r=10[mm]$

Rozwiązanie:

Dla układu z rysunku 7 należy wyznaczyć chwilowy środek obrotu, w sposób pokazany na rysunku 8.

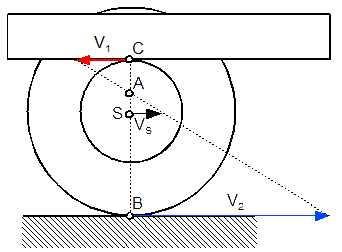
Najpierw znajdziemy położenie tymczasowego środka obrotu korzystając z następującej zależności:

[3]

Zapis wyrażenia w formacie TeX-a:

\frac{V_1+V_2}{|CB|}=\frac{V_1}{|AC|}\Rightarrow |AC|=\frac{V_1\cdot |CB|}{V_1+V_2}=6[mm]

Wykorzystując zasadę konstrukcji chwilowego środka obrotu obliczyć można prędkość liniową krążka V_S w następujący sposób:

[4]

Zapis wyrażenia w formacie TeX-a:

\frac{V_1}{|AC|}=\frac{V_S}{|CS|-|AC|}\Rightarrow V_S=\frac{V_1\cdot \left(|CS|-|AC|\right)}{|AC|}=6\frac{2}{3}\left[\frac{m}{s}\right]

Pozostało jedynie wyznaczyć prędkość kątową ω_S w następujący sposób:

[5]

Zapis wyrażenia w formacie TeX-a:

omega_s=\frac{V_S}{|CS|-|AC|}=1\frac{1}{9}\left[\frac{rad}{s}\right]

Zadanie 5

Obliczyć prędkość liniową tłoka połączonego z wałem korbowym silnika spalinowego obracającym się z zawrotną prędkością ω=5000[obr/min].

Rysunek do zadania 5 — Rys. 9
Korbowód i tłok silnika spalinowego.

Dane:

$omega=5000left[frac{obr}{min}right]=523.6left[frac{rad}{s}right]; L_1=100[mm];L_2=250[mm];alpha =30^o$

Rozwiązanie:

Najpierw wyznaczyć należy wektor prędkości V₁ w następujący sposób:

[6]

Zapis wyrażenia w formacie TeX-a:

V_1=\omega\cdot L_1=52360\left[\frac{mm}{s}\right]

W tym przypadku konstrukcja chwilowego środka obrotu jest niewygodna w użyciu (ale nie niemożliwa do wykorzystania) gdyż znając kąt α łatwiej jest zrzutować wektor prędkości V₁ na oś ruchu tłoka:

[7]

Zapis wyrażenia w formacie TeX-a:

V_{2}=V_1\cdot \sin\alpha=26180\left[\frac{mm}{s}\right]=94.248\left[\frac{km}{h}\right]