Równanie dynamiczne ruchu obrotowego
Konstrukcja chwilowego środka obrotu
Masowy moment bezwładności punktu materialnego
Równanie dynamiczne ruchu obrotowego
Równanie dynamiczne ruchu prostoliniowego
Obliczenie przyspieszeń układów ciał metodą Newtona
Zasada równowagi pracy i energii
Obliczenia układów dynamicznych metodą równoważności energii i pracy
Ogólne równanie dynamiki d'Alamberte'a Lagrange'a
Obliczenia układów dynamicznych metodą prac przygotowawczych
Ta strona należy do działu:
poddziału
Dynamika Autor podstrony: Krzysztof Zajączkowski
Stronę tą wyświetlono już: 7974 razy
Pochodna krętu KZ ciała po czasie jest równa sumie momentów obrotowych MZ względem osi Z :
[1]
Zapis wyrażenia w formacie TeX-a:
\frac{dK_z}{dt}=\sum_{i=1}^{n}M_{iz}
Kręt ciała względem osi Z jego obrotu jest równy iloczynowi odśrodkowego masowego momentu bezwładności IZ oraz prędkości kątowej ω .
[2]
Zapis wyrażenia w formacie TeX-a:
K_Z=I_Z\cdot \omega
Podstawiając równanie [2] do równania [1] otrzymujemy:
[3]
Zapis wyrażenia w formacie TeX-a:
I_Z\cdot \frac{d\omega}{dt}=\sum_{i=1}^{n}M_{iz}
Pochodna prędkości kątowej ω po dt jest niczym innym niż przyspieszeniem kątowym ε , więc ostatecznie równanie [3] przyjmuje następującą postać:
[4]
Zapis wyrażenia w formacie TeX-a:
I_Z\cdot \varepsilon =\sum_{i=1}^{n}M_{iz}
W powyższych równaniach wyrażenie MiZ może być momentem obrotowym M lub siłą P przemnożoną przez promień r jej działania względem środka obrotu.
Zadanie 1
Obliczyć przyspieszenie kątowe koła zamocowanego obrotowo w środku ciężkości jak na rysunku 1 .
Rysunek koła zamocowanego obrotowo w środku ciężkości i obciążonego momentem obrotowym i siłami.
Dane:
Rozwiązanie:
Zastosować należy tutaj równanie [4] oraz równanie [8] z strony Mechanika techniczna → Dynamika → Masowy moment bezwładności punktu materialnego masowego momentu bezwładności IZ dla walca.
[5]
Zapis wyrażenia w formacie TeX-a:
\frac{1}{2}\cdot m\cdot r^2\cdot \varepsilon = M + P_1\cdot r - P_2\cdot r
Równanie [5] jest równaniem dynamicznej równowagi ruchu obrotowego dla układu z rysunku 1 . Z tego równania wyznaczamy przyspieszenie kątowe ε i obliczamy jego wartość w następujący sposób:
[6]
Zapis wyrażenia w formacie TeX-a:
\varepsilon = \frac{M + P_1\cdot r - P_2\cdot r}{\frac{1}{2}\cdot m\cdot r^2}=1\frac{2}{5}\left[\frac{rad}{s}\right]
Tematy powiązane
![r=frac{1}{2}[m];m=100[kg]; P_1=10[kN]; P_2=15[kN]; M=20[Nm]](rownania/w_571.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_572.gif)

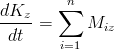

![Podstawienie równanie [2] do równania [1]](https://obliczeniowo.com.pl/rownania/w_569.gif)
![ostateczna postać równania [3]](https://obliczeniowo.com.pl/rownania/w_570.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_573.gif)