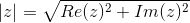Moduł i argument liczby zespolonej

Stronę tą wyświetlono już: 6968 razy

Moduł jak i argument liczby zespolonej jest ściśle powiązany z zapisem trygonometrycznym tejże liczby. Albowiem za prawdę powiadam wam, że liczbę zespoloną można zapisać z wykorzystaniem modułu (czyli długości wektora, jakim wszakże jest liczba zespolona) oraz argumentu (czyli kąta φ zawartego pomiędzy osią liczb rzeczywistych Re a liczbą zespoloną.

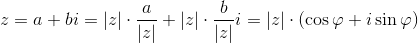[1]

Zapis wyrażenia w formacie TeX-a:

z = a + bi = |z|\cdot\frac{a}{|z|} + |z|\cdot\frac{b}{|z|}i = |z|\cdot(\cos \varphi + i\sin \varphi)

Graficznie przedstawienie modułu i argumentu liczby zespolonej pokazane zostało na poniższym rysunku.

Moduł i argument liczby zespolonej są współrzędnymi układu biegunowego liczby zespolonej. Obliczenie modułu sprowadza się do zastosowania starego dobrego Twierdzenia Pitagorasa:

[2]

Zapis wyrażenia w formacie TeX-a:

|z|=\sqrt{Re(z)^2+Im(z)^2}

gdzie:

• Re(z) - funkcja specjalna, która zwraca wartość części rzeczywistej liczby zespolonej;
• Im(z) - funkcja specjalna, która zwraca wartość części urojonej liczby zespolonej;

Nieco trudniej jest w przypadku obliczania argumentu liczby zespolonej, do tego celu można posłużyć się funkcją tangens w następujący sposób:

[3]

Zapis wyrażenia w formacie TeX-a:

\varphi=\begin{cases} \operatorname{arc tg}\left(\frac{b}{a}\right), & \mbox{gdy } a > 0 \\ \operatorname{arc tg}\left(\frac{b}{a}\right)+\pi, & \mbox{gdy }a < 0 \\ 0, & \mbox{gdy }a = 0\, oraz \, b > 0 \\ \pi, & \mbox{gdy }a = 0\, oraz \, b < 0 \end{cases}