Mnożenie liczb zespolonych zapisanych w postaci trygonometrycznej

Stronę tą wyświetlono już: 5230 razy

Mnożenie liczb zespolonych zapisanych w postaci trygonometrycznej wykazuje pewne ciekawe właściwości, które pokrótce postaram się omówić na ogólnym przykładzie mnożenia dwóch liczb zespolonych z₁ i z₂:

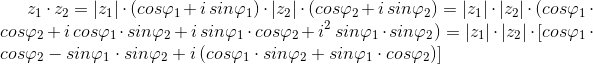[1]

Zapis wyrażenia w formacie TeX-a:

z_1\cdot z_2=|z_1|\cdot(cos\varphi_1+i\,sin\varphi_1)\cdot|z_2|\cdot(cos\varphi_2+i\,sin\varphi_2)=|z_1|\cdot|z_2|\cdot(cos\varphi_1\cdot cos\varphi_2 + i\, cos\varphi_1\cdot sin\varphi_2+i\,sin\varphi_1\cdot cos\varphi_2+i^2\,sin\varphi_1\cdot sin\varphi_2)=|z_1|\cdot|z_2|\cdot[cos\varphi_1\cdot cos\varphi_2-sin\varphi_1\cdot sin\varphi_2 + i\,(cos\varphi_1\cdot sin\varphi_2+sin\varphi_1\cdot cos\varphi_2)]

Powyższy wzór niczym Angela Merkel na razie nie zachwyca swoją urodą, ale poczekajcie chwilę, a stanie się on motylem! Albowiem za prawdę powiadam wam, że z funkcji trygonometrycznych można zastosować tutaj wzory na sumę kątów:

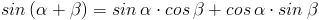[2]

Zapis wyrażenia w formacie TeX-a:

\sin\left(\alpha+\beta\right)=\sin\,\alpha\cdot \cos\,\beta +\cos\,\alpha\cdot \sin\,\beta

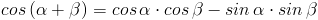[3]

Zapis wyrażenia w formacie TeX-a:

\cos\left(\alpha+\beta\right)=\cos\,\alpha\cdot \cos\,\beta-\sin\,\alpha\cdot \sin\,\beta

Tak więc wykorzystując zależności [2] i [3] do [1] otrzymuje się następujący wzór:

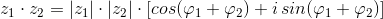[4]

Zapis wyrażenia w formacie TeX-a:

z_1\cdot z_2=|z_1|\cdot|z_2|\cdot[cos(\varphi_1+\varphi_2)+i\,sin(\varphi_1+\varphi_2)]

Cóż za ciekawy wzór! Okazuje się, że otrzymana liczba iloczynu ma moduł równy iloczynowi modułów mnożonych liczb zaś argument jest równy sumie argumentów tychże liczb. Jakże daleko idące wnioski można z tego wzniosłego wydarzenia wyciągnąć? Ano takie, że mnożenie liczb zespolonych zapisanych w postaci trygonometrycznej jest prostsze niż odebranie dzieciakowi lizaka (aczkolwiek nigdy nie próbowałem odebrać żadnemu dzieciakowi lizaka więc w tej kwestii mogę się mylić).