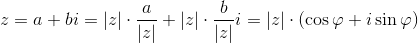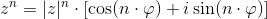Potęgowanie liczb zespolonych

Stronę tą wyświetlono już: 1643 razy

Potęgowanie liczb zespolonych najłatwiej jest zrealizować, gdy liczba ta jest zapisana w postaci geometrycznej:

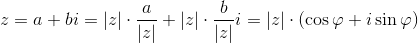[1]

Zapis wyrażenia w formacie TeX-a:

z = a + bi = |z|\cdot\frac{a}{|z|} + |z|\cdot\frac{b}{|z|}i = |z|\cdot(\cos \varphi + i\sin \varphi)

Wtedy to bowiem wystarczy podnieść do potęgi n moduł |z| owej liczby oraz przemnożyć jej argument ϕ przez n w następujący sposób:

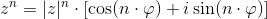[2]

Zapis wyrażenia w formacie TeX-a:

z^n=|z|^n\cdot[\cos (n\cdot\varphi) + i\sin (n\cdot\varphi)]

Powyższy wzór nazywany jest wzorem de Moivre'a i jest on spełniony dla liczby n należącej do zbioru liczb całkowitych.