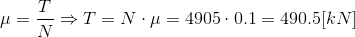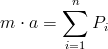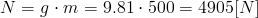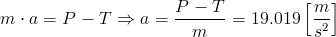Równanie dynamiczne ruchu prostoliniowego

Stronę tą wyświetlono już: 2174 razy

Dla ciała poruszającego się ruchem jednostajnie przyspieszonym można zapisać równanie dynamiczne ruchu prostoliniowego:

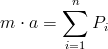[1]

Zapis wyrażenia w formacie TeX-a:

m\cdot a=\sum_{i=1}^n\P_i

gdzie:

• m - masa ciała;
• a - przyspieszenie liniowe;
• P_i - siły wywołujące i przeciwdziałające ruchowi.

Zadanie 1

Obliczyć przyspieszenie liniowe ciała poruszającego się po płaskiej poziomej chropowatej powierzchni pod wpływem działania siły P.

Dane:

Rozwiązanie:

Zacznijmy od wyznaczenia siły nacisku N zależnej od masy ciała m i przyspieszenia ziemskiego g:

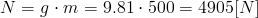[2]

Zapis wyrażenia w formacie TeX-a:

N=g\cdot m=9.81\cdot 500=4905[N]

Tarcie wyznaczyć trzeba z zależności następującej:

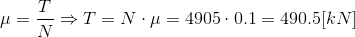[3]

Zapis wyrażenia w formacie TeX-a:

\mu=\frac{T}{N}\Rightarrow T=N\cdot \mu = 4905 \cdot 0.1 = 490.5[kN]

Równanie dynamiczne ruchu prostoliniowego:

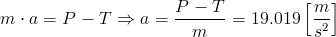[4]

Zapis wyrażenia w formacie TeX-a:

m\cdot a=P-T\Rightarrow a=\frac{P-T}{m}=19.019\left[\frac{m}{s^2}\right]

Komentarze