Stronę tą wyświetlono już: 13596 razy

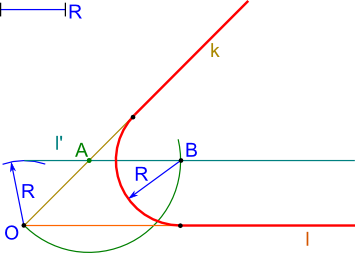
Dwie półproste k i l mają wspólny punkt początkowy O, należy zaokrąglić kąt zawarty pomiędzy tymi półprostymi łukiem o promieniu R. Za pomocą cyrkla z punktu O należy zakreślić łuk, a następnie przy pomocy ekierek wyznaczyć prostą równoległą do półprostej l. Z punktu A przecięcia się prostej l' z półprostą k promieniem o rozwartości równej długości odcinka AO wyznaczyć punkt B będący środkiem okręgu o promieniu R stycznego do półprostych k oraz l.

W powyższej konstrukcji można zastosować do wyznaczenia prostej równoległej l' konstrukcję z strony Geometria wykreślna → Podstawowe konstrukcje → Kreślenie prostych równoległych.