Okrąg wpisany w trójkąt
Stronę tą wyświetlono już: 6403 razy
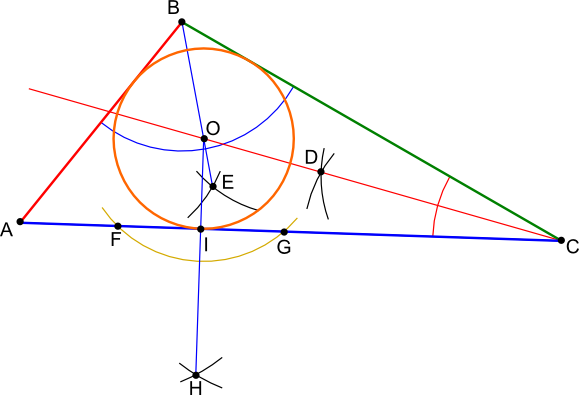
Środek okręgu wpisanego w trójkąt wyznacza punkt przecięcia siecznych kątów trójkąta jak na rysunku 1. Sieczna kąta jest to nic innego jak podział kąta na dwie równe części, a konstrukcja takiego podziału była już omawiana wcześniej. Promień okręgu wyznaczy nam prostopadły rzut na jeden z boków trójkąta środka okręgu O. W celu zrzutowania punktu O zakreślić należy łuk wyznaczający punkty F, G z których to z kolei wyznaczony zostanie punkt H. Połączenie punktu H z punktem O daje prostą prostopadłą do boku AC trójkąta i wyznacza punkt I, którego odległość od środka okręgu O jest promieniem okręgu wpisanego w trójkąt.
Rys. 1
Okrąg wpisany w trójkąt.