Stronę tą wyświetlono już: 12202 razy

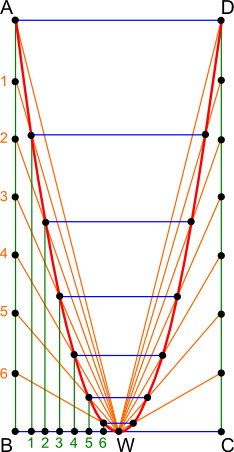
Konstrukcja kreślenia paraboli opiera się (jak zresztą widać na rysunku 1) na prostokącie ABCD którego dłuższy bok podzielony został na siedem równych części. Krótszy bok został podzielony na dwie równe części, a jedna z tych części podzielona została z kolei na siedem równych części. Połączenie punktu W z punktami leżącymi na dłuższych bokach prostokąta tworzy część siatki niezbędnej do wyznaczenie punktów, przez które przechodzi parabola. Drugą część sitaki stanowić będą linie równoległe do dłuższych boków prostokąta ABCD i wychodzące z punktów podziału połowy krótszego boku tego prostokąta. Punkty przecięcia prostych przechodzących przez punkty o tych samych numerach to punkty przejścia paraboli. Oczywiście owe punkty należy interpolować, np. za pomocą tajemniczego przyrządu zwanego krzywikiem.

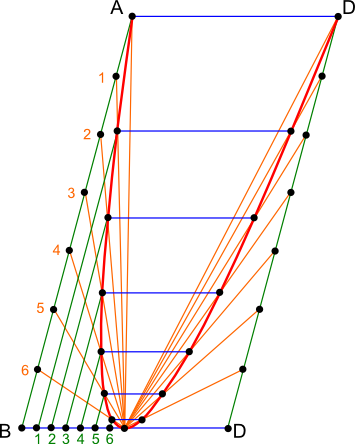
Nie ulega wątpliwości, że możliwe jest narysowanie paraboli pochyłej jak na rysunku 2, wystarczy tylko przenieść tą samą konstrukcję co na rysunku 1 na równoległobok.