Kreślenie hipocykloidy

Stronę tą wyświetlono już: 6490 razy

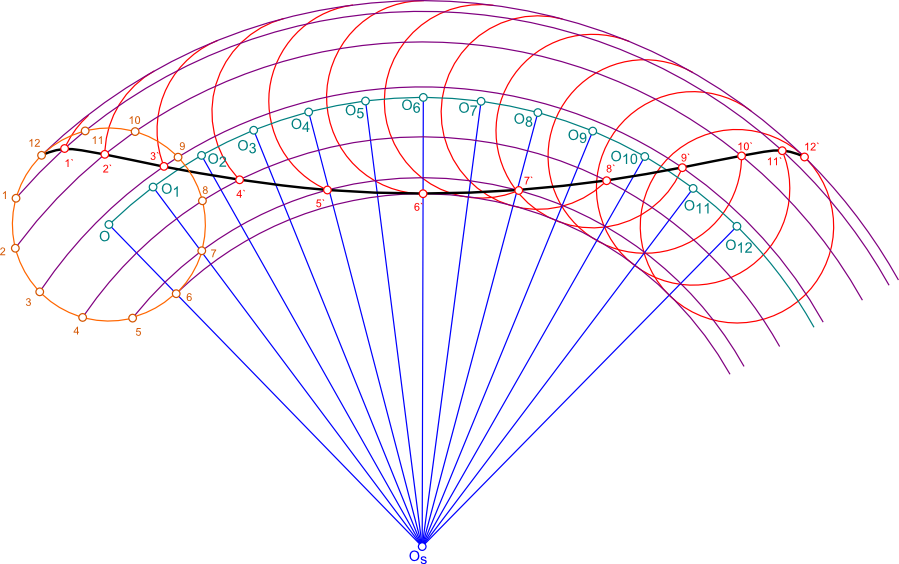
Hipocykloida to krzywa jaką kreśli punkt znajdujący się na obwodzie koła toczącego się bez poślizgu po wewnętrznej stronie drugiego koła. Hipocykloidę wyznacza się poprzez obranie punktu środka okręgu O_S po którym będzie się toczyło koło z punktem rysującym hipocykloidę (jak na rysunku 1). Należy obrać dowolny promień O_S1 okręgu oraz mniejszy promień O-1 okręgu toczącego się po okręgu większym. Z punktu przecięcia się odcinka O_SO z nakreślonym okręgiem należy dokonać jego podziału na dwanaście równych części. Dla każdego z dwunastu punktów podziału należy z punktu O_S zakreślić łuki będące pierwszą częścią siatki wyznaczającej punkty przejścia hipocykloidy. Dodatkowo należy nakreślić łuk z punktu O_S od punktu O, na którym dowolną równą rozwartością cyrkla należy odmierzyć dwanaście odcinków, wyznaczających kolejne punkty przemieszczenia środka toczącego się okręgu. Dla każdego punktu O_{1 do 12} należy zakreślić łuki do kolejno następujących po sobie punktów przecięcia. Owe punkty są punktami przejścia hiperboli i należy je połączyć krzywą za pomocą krzywików.