Rzuty Monge'a
Stronę tą wyświetlono już: 42124 razy
Metoda Monge'a prostopadłego rzutowania punktów na prostopadłe płaszczyzny rzutowania (rzutnie) jest powszechnie stosowaną metodą jednoznacznego przedstawiania obiektów trójwymiarowych na płaszczyźnie. Rysunek techniczny opiera się na metodzie Monge'a, stosując tą metodę do tworzenia dokumentacji technicznych produkowanych przedmiotów.
Mając dwa prostopadłe rzuty danego przedmiotu, można uzyskać rzut tego przedmiotu w dowolnej perspektywie. Na rysunku 1 można zobaczyć trójwymiarowy obiekt, zrzutowany na dwie prostopadłe do siebie rzutnie.
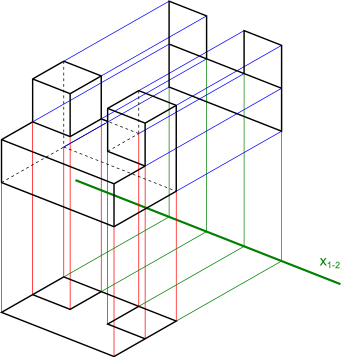
Rozwinięcie rzutni z rysunku 1 można obejrzeć na rysunku 2. Jak już wcześniej pisałem, informacje zawarte na rysunku 2 można wykorzystać w celu uzyskania dowolnego widoku przedmiotu, który owe rzuty dotyczą.
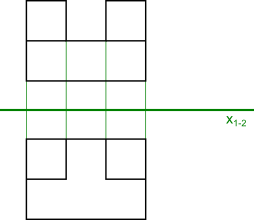
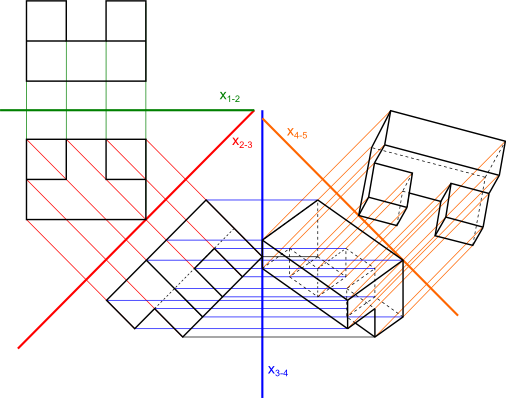
Dla przykład na rysunku 3 można obejrzeć kilka kolejnych rzutów przedmiotu z rysunku 1 i 2. W rzutowaniu metodą Monge'a długości krawędzi przedmiotu ulegają skróceniu, gdy patrzy się na nie pod innym kątem niż 90°. Skrócenie to można wyrazić stosunkiem długości rzeczywistej danej krawędzi, do jej długości w danym rzucie. Wartość ta zawierać się może w zakresie wartości od 0 do 1.
Zasada rzutowania jest prosta, dla każdego z rzutowanych punktów należy poprowadzić proste prostopadłe do osi rzutni (np. x2-3). Położenie punktu na danej linii można odczytać z wcześniejszej rzutni, czyli dla rozpatrywanego przypadku z rzutni x1-2, gdzie odległość rzutowanego punktu od osi x1-2 jest położeniem tego punktu względem osi x2-3 na linii rzutowania.
Metodą rzutów Monge'a możliwe jest wyznaczenie punktu przebicia płaszczyzny prostą, bądź też linii przenikania się dwóch płaszczyzn, jak również wyznaczenie długości boków rzutowanych brył co z kolei umożliwia stworzenie siatki płaskiej takiej bryły. Aby jednak możliwe było wyznaczenie tych wszystkich właściwości na podstawie rzutów danej bryły konieczne jest poznanie kilku ważnych praw rzutowania. O tych właśnie prawach i nie tylko będzie mowa w tym dziale.
