Stronę tą wyświetlono już: 12599 razy

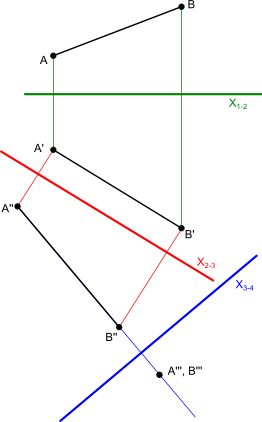
Zdarza się czasami, że konieczne jest wyznaczenie rzeczywistej długości odcinka lub długości boków danej powierzchni rzutowanego obiektu. Aby było to możliwe konieczne jest zrzutowania danego obiektu w odpowiedni sposób. Dla dowolnego odcinka AB, którego dwa podstawowe rzuty są znane (rys. 1) można znaleźć jego rzeczywistą długość ustawiając rzutnię x_2-3 równolegle do tego odcinka. Ustawiając rzutnię x_3-4 prostopadle do odcinka AB uzyskuje się jego zwinięcie do punktu (punkty A oraz B się pokrywają).

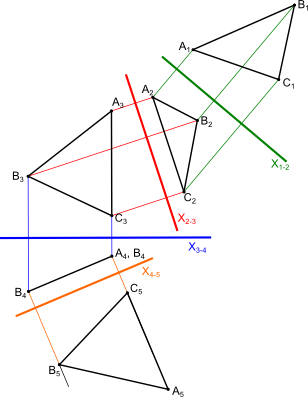
Wyznaczenie rzeczywistych długości boków płaszczyzny ABC z rysunku 2 możliwe jest poprzez uzyskanie rzutu prostopadłego a następnie równoległego do tej płaszczyzny. Uzyskanie tych rzutów jest możliwe dzięki wykorzystaniu konstrukcji zwijania linii do punktu rozrysowanej na rysunku 1.

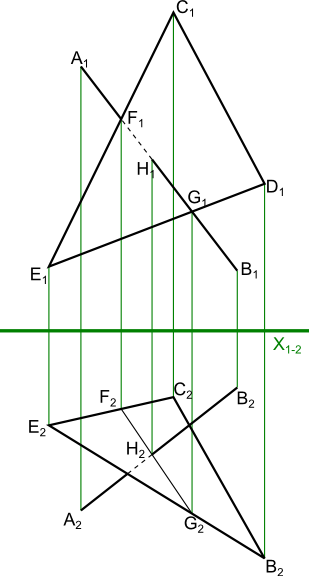
Zdarza się czasami, że trzeba wyznaczyć punkt przenikania prostej lub odcinka AB z płaszczyzną CDE jak na rysunku 3. W takich przypadkach konieczne jest wyznaczenie śladu odcinka AB na jednym z rzutów płaszczyzny CDE. W tym celu należy znaleźć punkty F oraz G przecięcia się odcinka AB z krawędziami płaszczyzny CDE, a następnie zrzutowanie ich na odpowiednie krawędzie tej płaszczyzny znajdujące się na drugim rzucie. Połączenie uzyskanych w ten sposób punktów ukaże nam punkt przebicia płaszczyzny CDE odcinkiem AB.

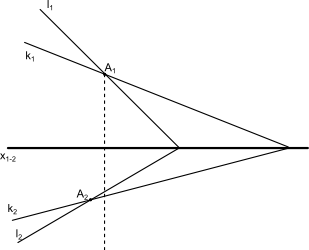
Kolejną właściwością rzutowania jest warunek współpłaszczyznowości linii. Obierzmy więc czym prędzej dwie proste k oraz l, których rzuty są równoległe. Takie linie są współpłaszczyznowe, ponieważ rzuty linii niewspółpłaszczyznowych zawsze przecinają się na co najmniej jednej z rzutni. Na rysunku 4 pokazany został przypadek linii równoległych, które są również równoległe na płaszczyźnie, którą wyznaczają.

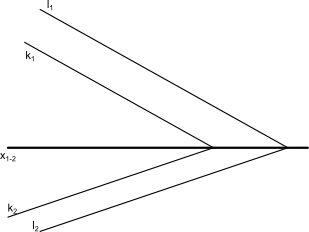
Jest też inny przypadek, gdy linie k i l wyznaczają płaszczyznę. Takim przypadkiem pokazanym na rysunku 5 są linie, które mają wspólny punkt przecięcia pokrywający się na obu rzutniach.

Ostatni przypadek, to sytuacja, gdy linie k i l nie są ani równoległe względem siebie na danej rzutni, ani nie mają wspólnego punktu przecięcia, który by się pokrywał na obu rzutniach. Taki przypadek można zobaczyć na rysunku 6.