Twierdzenie Talesa

Stronę tą wyświetlono już: 12627 razy

Twierdzenie Talesa, tak, tak tego Talesa z Miletu o którym każdy słyszał w podstawówce i nie tylko:

Jeżeli ramiona przecinają dwie proste k i m spełniające warunek wzajemnej równoległości, to stosunek odcinków wyznaczonych przez te proste na jednym ramieniu kąta jest równy stosunkowi odpowiednich odcinków z drugiego ramienia kąta.

[1]

Zapis wyrażenia w formacie TeX-a:

\frac{\left|AB\right|}{\left|AC\right|}=frac{left|AD\right|}{\left|AE\right|}=frac{left|BD\right|}{left|CE\right|}

Przekształcając pary członów równania [1] można uzyskać dodatkowe zależności wynikające z twierdzenia Talesa:

[2]

Zapis wyrażenia w formacie TeX-a:

\frac{\left|AB\|ight|}{\left|AD\right|}=\frac{\left|AC\right|}{left|AE\right|}

[3]

Zapis wyrażenia w formacie TeX-a:

\frac{\left|AB\right|}{\left|BD\right|}=\frac{\left|AC\right|}{left|CE\right|}

[4]

Zapis wyrażenia w formacie TeX-a:

\frac{\left|BD \right|}{\left|AD\right|}=\frac{\left|CE\right|}{\left|AE\right|}

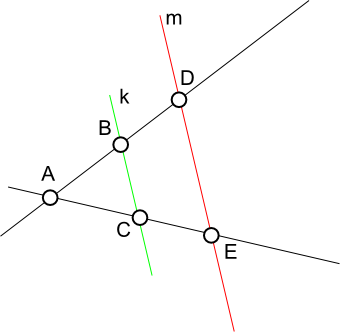
Dowód słuszności twierdzenia Talesa

Stosunek pól powierzchni widoczny na rysunku 1 trójkątów ΔABC oraz ΔBDC jest równy stosunkowi długości |AB| oraz |BD|:

[5]

Zapis wyrażenia w formacie TeX-a:

\frac{p,\Delta ABC}{p,\Delta BDC}=\frac{\frac{1}{2}\cdot h\cdot \left|AB\right|}{\frac{1}{2}\cdot h\cdot \left|BD\right|}=\frac{|AB|}{|BD|}

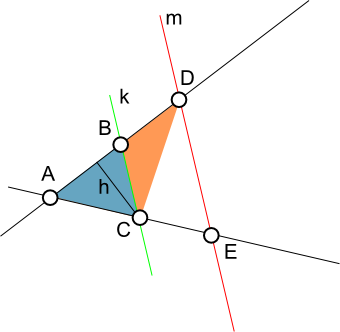
Analogicznie do rysunku 1 można na podstawie rysunku 2 napisać następującą zależność:

[6]

Zapis wyrażenia w formacie TeX-a:

\frac{p,\Delta ABC}{p,\Delta CBE}=\frac{\frac{1}{2}\cdot h_2\cdot \left|AC\right|}{\frac{1}{2}\cdot h_2\cdot \left|CE\right|}=\frac{|AC|}{|CE|}

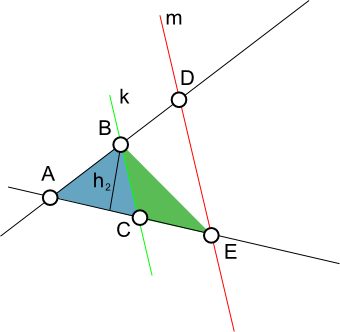
Teraz należy jeszcze zauważyć, że trójkąty ΔBCD z rysunku 2 oraz ΔBCE z rysunku 3 mają tą samą wysokość i wspólny bok |BC|, w związku z czym pola powierzchni tych trójkątów są sobie równe:

[7]

Zapis wyrażenia w formacie TeX-a:

p, \Delta CBD = p, \Delta BCE

Z zależności [7] wynika następna równość, będąca zlepkiem zależności [5] i [6]:

[8]

Zapis wyrażenia w formacie TeX-a:

\frac{p,\Delta ABC}{p,\Delta BDC} = \frac{p,\Delta ABC}{p,\Delta CBE} = \frac{|AB|}{|BD|} = \frac{|AC|}{|CE|}

W analogiczny sposób można dowieść każdą z zapisanych zależności [1], [2], [3] i [4].

Twierdzenie Talesa w geometrii wykreślnej

Kto nie stosował twierdzenia Talesa w celu podziału odcinka na części? W geometrii wykreślnej jest to jedna z podstawowych konstrukcji, która w niejednym przypadku się przydaje. Na rysunku 4 można zobaczyć sposób jej zastosowania, polegający na poprowadzeniu z punktu końcowego A odcinka AB linii pomocniczej oraz podzieleniu tej linii za pomocą cyrkla na tyle części, na ile ma być podzielony odcinek AB. Następnie łączymy ekierką ostatni punkt podziału linii pomocniczej z punktem B i przesuwając równolegle ekierkę do kolejnych punktów podziału linii pomocniczej odrysować linie aż do ich przecięcia z odcinkiem AB.

Poniżej można obejrzeć konstrukcje geometryczne, w których zastosowanie twierdzenia Talesa odgrywa kluczową rolę.

Twierdzenie Talesa a twierdzenia o podobieństwie trójkątów

Istnieją trzy twierdzenia o podobieństwie trójkątów, które w zasadzie wynikają z twierdzenia Talesa:

Twierdzenie 1

Dwa trójkąty są podobne, jeżeli długości dowolnych dwóch boków jednego trójkąta są proporcjonalne do odpowiednich długości boków trójkąta drugiego, a kąty zawarte pomiędzy tymi bokami są sobie równe.

Twierdzenie 2

Dwa trójkąty są podobne, gdy kąty jednego trójkąta są odpowiednio równe kątom trójkąta drugiego.

Twierdzenie 3

Dwa trójkąty są podobne, gdy trzy boki jednego trójkąta są proporcjonalne do odpowiadających im boków trójkąta drugiego.

Pomiar wysokości konstrukcji i budynków

Twierdzenie Talesa można zastosować do pomiaru wysokości budynków lub innych obiektów naziemnych. Dla przykładu weźmy maszt, którego wysokość chcemy zmierzyć (rys. 8), oraz listewkę wbitą prostopadle w ziemię, której wysokość od powierzchni ziemi jest znana. Należy dokonać pomiaru długości rzucanych cieni przez maszt i listewkę.

Cienie powstałe od promieni słonecznych dla naszych obiektów naziemnych są proporcjonalne do ich wysokości, a co za tym idzie trójkąty zbudowane na wysokości h₁ i długości cienia L₁ oraz h₂ i L₂ są podobne, ponieważ kąt zawarty między nimi wynosi 90°. Prawdziwa jest zatem następująca zależność:

[9]

Zapis wyrażenia w formacie TeX-a:

\frac{h_1}{L_1}=\frac{h_2}{L_2}\Rightarrow h_1 = L_1\cdot \frac{h_2}{L_2}

Pomiarów długości cieni należy dokonać jednocześnie, aby pomiary były w miarę dokładne, ponieważ ziemia się kręci wokół własnej osi (i nie tylko), a co za tym idzie położenie Słońca na sklepieniu niebieskim się zmienia i zmienia się też długość cienia.

Wysokość lotu samolotu pasażerskiego

Jeśli przyszło Ci kiedykolwiek do głowy aby się zastanowić nad tym, na jakiej wysokości przelatują nad naszymi głowami samoloty pasażerskie, to twierdzenie Talesa jest w stanie Ci pomóc w odpowiedzi na to pytanie. Na rysunku 9 widoczny jest taki właśnie samolot zrobiony w 18-krotnym powiększeniu, co oznacza że wygląda on tak jakby leciał na 18-krotnie mniejszej wysokości. Naniesiona na zdjęcie podziałka jest po prostu wrysowana przeze mnie, spowodowane jest to faktem, że aby umieścić na zdjęciu samolotu podziałkę rzeczywistą musiałbym jednocześnie trzymać linijkę w odpowiedniej odległości od obiektywu i aparat tak aby była widoczna podziałka linijki jak i samolot. Nie muszę chyba tłumaczyć, że wykonanie takiego zdjęcia w dobrej jakości przez jedną osobę graniczy z cudem.

Umówmy się że samolot z rysunku 9 Boeing 737-400, którego długość rzeczywista wynosi h_rs=28.88[m], na podziałce samolot ten ma jednak jedynie h_ps=14[mm] długości, co w przeliczeniu na metry daje w_ps=0.014[m]. Załóżmy, że podziałka samolotu w trakcie robienia tego zdjęcia znajdowała się w odległości h_ps=1[m] od matrycy aparatu. Można zapisać następującą zależność:

[10]

Zapis wyrażenia w formacie TeX-a:

\frac{h_{rs}}{w_{rs}}=\frac{h_{ps}}{w_{ps}}\Rightarrow h_{rs}=w_{rs}\cdot\frac{h_{ps}}{w_{ps}}

Po podstawieniu naszych danych do wzoru [10] uzyskuje się wysokość rzeczywistą samolotu h_rs=2063[m].

Obliczenie odległości od obserwowanego obiektu

Załóżmy taką oto hipotetyczną sytuację: przy jednej z krawędzi drogi stoi czołg jak na rysunku 10 obserwator znajdujący się początkowo blisko znaku drogowego umieszczonego w punkcie A chce dowiedzieć się, w jakiej odległości L₁ stoi czołg. W tym celu stwierdził, że droga ma szerokość równą ośmiu półmetrowym krokom, następnie oddalił się od znaku wzdłuż drogi o odległość L₂=16 kroków a następnie obracając się o 90° przemieścił się o trzy kroki, gdyż w tym położeniu zauważył, że czołg i znak drogowy leżą w jednej linii.

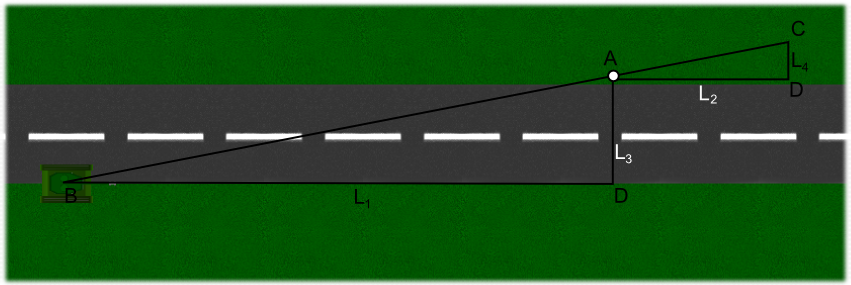
Po wykonaniu serii niezwykle zaawansowanych pomiarów, nasz obserwator ułożył następującą zależność:

[11]

Zapis wyrażenia w formacie TeX-a:

\frac{L_1}{L_3}=\frac{L_2}{L_4}\Rightarrow L_1=L_3\cdot\frac{L_2}{L_4}

Podstawiając więc do równania [11] wartości odległość L₁=42 i 2 / 3 półmetrowych kroków co daje 21 i 1/3[m].

Graficzne wyznaczanie iloczynu i ilorazu dwóch liczb

A niechaj będą takie dwie dowolne rzeczywiste liczby a i b, których wartości wyznaczają długości odcinków o tych samych nazwach i niechaj będzie dany odcinek j, taki że jego długość wynosi 1 (opcjonalnie dowolnej obranej jednostki długości). W takim przypadku możliwe jest graficzne wyznaczenie odcinka c, którego długość będzie odpowiadała iloczynowi długości boków a i b.

Wyznaczenie odcinka c wymaga jedynie zastosowania konstrukcji geometrycznej pokazanej na poniższej ilustracji.

Powyższa konstrukcja może być uzasadniona za pomocą twierdzenia Talesa w następujący sposób:

[12]

Zapis wyrażenia w formacie TeX-a:

\cfrac{c}{a}=\cfrac{b}{j}\Rightarrow c=a\cdot\cfrac{b}{j}

Ponieważ wiadomo nam, że odcinek j ma długość równą 1 przeto równanie [12] sprowadza się do postaci iloczynu długości odcinków a i b.

W jakże przebiegle podobny sposób można zastosować podobną konstrukcję dla ilorazu dwóch liczb c i b otrzymując w ten sposób odcinek a. Tak się cudownie wręcz składa, że konstrukcja z rysunku 11 doskonale nadaje się również do przeprowadzania tego typu "obliczeń" matematycznych.

Na koniec, mogę dodać, że możliwe jest pomnożenie dowolnej liczby a przez iloraz dwóch d i b w sposób pokazany na poniższej ilustracji.

Zakończenie

Ponad 2,5 tysiąca lat temu żył sobie człowiek, który odkrył i udowodnił twierdzenie o proporcjonalności odcinków powstałych z przecięć dwóch prostych równoległych z ramionami kąta. Człowiek ów potrafił również zastosować owo twierdzenie w praktyce, mierząc wysokość piramidy egipskiej, czy odległość statku od portu. W czasach gdy on tego dokonał, takie rzeczy robiły na zwykłych ludziach olbrzymie wrażenie, a przecież w dzisiejszych czasach większość ludzi nie zdaje sobie sprawy z potęgi twierdzenia Talesa i z powodzeniem można na nich wywrzeć podobne wrażenie jak niegdyś robił to sam Tales.