Obliczanie punktu zderzenia figur płaskich
Stronę tą wyświetlono już: 2712 razy
Kawał czasu temu (cokolwiek to oznacza) napisałem program, który w wymyślony od podstaw przeze mnie sposób oblicza punkt zderzenia dwóch obiektów płaskich. Cały algorytm powstał w oparciu o obliczenie punktu zderzenia dwóch punktów P1 oraz P2, które poruszają się z prędkościami określonymi wektorami V1 oraz V2. Zanim jednak uchylę rąbka tajemnicy dotyczącego tego algorytmu, opiszę pokrótce sam program, którego screen można obejrzeć na rysunku 1.
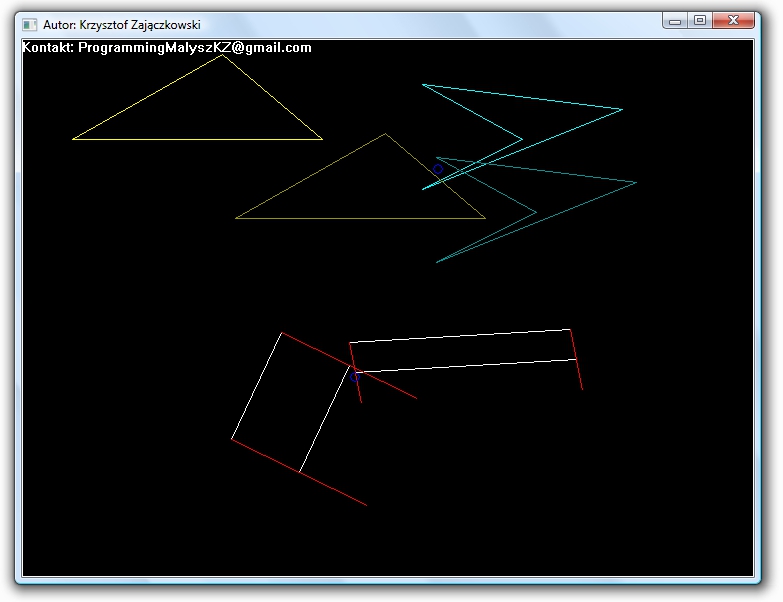
Na powyższym rysunku znajduję się dwa odcinki, które się przemieszczają z położenia początkowego do punktu zderzenia, oraz dwie figury płaskie również przemieszczające się do punktu zderzenia z pozycji początkowej. W programie wyświetlają się również dwa nieruchome odcinki i figury płaskie, które określają położenie początkowe obiektów zderzających się. Poniżej znajduje się krótka wideo prezentacja programu.
Jak widać na załączonej wideo prezentacji, narysowane na czerwono linie to wektory prędkości, które można zmieniać wedle uznania. Położenie końców odcinków również można zmieniać a wszystko to poprzez naciśnięcie w pobliżu końca odcinka lewego przycisku myszy i przesunięciu kursora myszy.
Wyznaczenie punktu zderzenia dla dwóch punktów P1 oraz P2 można dokonać za pomocą następującego równania, które jest prawdziwe, gdy punkty się zderzą:
Gdy dla wyliczonej wartości t pierwsza równość jest spełniona, to punkty się zderzą z sobą. W ten sposób można stwierdzić, czy dwa punkty się zderzą czy nie, kiedy się zderzą i gdzie się zderzą również. Zasada ta sprawdza się także dla trójwymiarowych współrzędnych kartezjańskich. Może się to wydawać dziwne lecz zależność [1] jest podstawą do stworzenia algorytmu obliczającego punkt zderzenia odcinka z punktem, a następnie odcinka z odcinkiem by w końcu umożliwić obliczenie punktu zderzenia wielokąta z wielokątem, punktem lub odcinkiem.
Zależność [1] jest wszystkim co tak naprawdę jest potrzebne do obliczania kolizji, ale aby zrozumieć jak go wykorzystać i jak jest to możliwe, trzeba to rozrysować i zrozumieć, jak to działa, a tę przyjemność proszę Państwa zostawiam Wam, cobyście się nie nudzili i trochę nad tym pogłowili. Pytanie brzmi: jak wykorzystać zależność [1] do obliczenia punktu zderzenia linii z punktem (reszta będzie już oczywista).

Tytuł:
C++ Zbiór zadań z rozwiązaniami
Autor:
Tomasz Jaśniewski

Tytuł:
Mikrokontrolery dla hobbystów. Projekty DIY w języku C i C++
Autor:
Miguel Angel Garcia-Ruiz, Pedro Cesar Santana Mancilla

Tytuł:
Architektura oprogramowania bez tajemnic. Wykorzystaj język C++ do tworzenia wydajnych aplikacji i systemów
Autor:
Adrian Ostrowski, Piotr Gaczkowski

Tytuł:
Wprowadzenie do C++
Autor:
Michał Matlak

Tytuł:
Opus magnum C++ 11. Programowanie w języku C++. Wydanie II poprawione (komplet)
Autor:
Jerzy Grębosz

Tytuł:
Programowanie wieloplatformowe z C++ i wxWidgets 3
Autor:
Bartosz W. Warzocha

Tytuł:
Język C++ i przetwarzanie współbieżne w akcji. Wydanie II
Autor:
Anthony Williams

Tytuł:
C++ dla bystrzaków. Wydanie VII
Autor:
Stephen R. Davis

Tytuł:
Tablice informatyczne. Podstawy C++
Autor:
Radosław Sokół

Tytuł:
Opus magnum C++11. Programowanie w języku C++ (komplet)
Autor:
Jerzy Grębosz

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1795.gif)