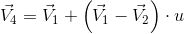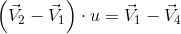Rzutowanie punktu na prostą
Stronę tą wyświetlono już: 7505 razy
Niech istnieją dwa wektory opisujące linię rzutowania V1 i V2 oraz rzutowany punkt V3. Konieczne jest następujące założenie: V1 ≠V2. Istnieje możliwość obliczenia wektora V4 będącego prostopadłym rzutem wektora V3 na prostą określoną wektorami V1 i V2 poprzez obliczenie współczynnika u za pomocą następującego wzoru:
 | [1] |
Zapis wyrażenia w formacie TeX-a:
będącego rozszerzeniem wzoru wykorzystującego iloczyn skalarny:
 | [2] |
Zapis wyrażenia w formacie TeX-a:
Współczynnik u jest stosunkiem długości wektora otrzymanego z różnicy wektorów V4-V1 do długości wektora otrzymanego z różnicy wektorów V2-V1 (rys. 1).
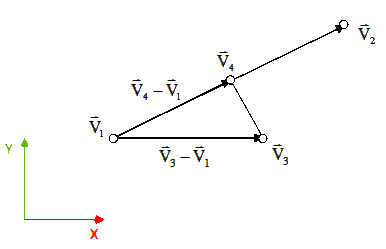
Znając więc wartość współczynnika u można obliczyć w współrzędne wektora V4 korzystając z operacji skalowania wektora V2-V1 przez wyliczony współczynnik u:
gdzie:

Tytuł:
Algorytmy. Ilustrowany przewodnik
Autor:
Aditya Bhargava

Tytuł:
Algorytmy. Struktury danych i złożoność obliczeniowa
Autor:
Feliks Kurp

Tytuł:
Algorytmy w Pythonie. Techniki programowania dla praktyków
Autor:
Piotr Wróblewski

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Algorytmy kryptograficzne w Pythonie. Wprowadzenie
Autor:
Shannon W. Bray

Tytuł:
Algorytmy sztucznej inteligencji. Ilustrowany przewodnik
Autor:
Rishal Hurbans

Tytuł:
Algorytmy bez tajemnic
Autor:
Thomas H. Cormen

Tytuł:
Algorytmy dla bystrzaków
Autor:
John Paul Mueller, Luca Massaron

Tytuł:
Algorytmy Data Science. Siedmiodniowy przewodnik. Wydanie II
Autor:
David Natingga

Tytuł:
Algorytmy uczenia maszynowego. Zaawansowane techniki implementacji
Autor:
Giuseppe Bonaccorso