Wyznaczanie punktu przecięcia dwóch prostych
Stronę tą wyświetlono już: 4861 razy
Niech istnieją dwa linie L1 oraz L2 opisane wektorami V1 i V2 dla linii V1 i V3, V4 dla linii L2. Konieczne jest następujące założenie: linia L1 nie jest równoległa do linii L2. Istnieje możliwość obliczenia wektora V5 będącego przecięciem dwóch linii L1, L2 poprzez wykorzystanie rzutowania prostopadłego wektorów, podobieństw trójkątów oraz skalowania wektorów. Aby dowiedzieć się więcej o rzutowaniu prostopadłym punktu na prostą należy przeczytać artykuł "Rzutowanie punktu prostopadle na prostą".
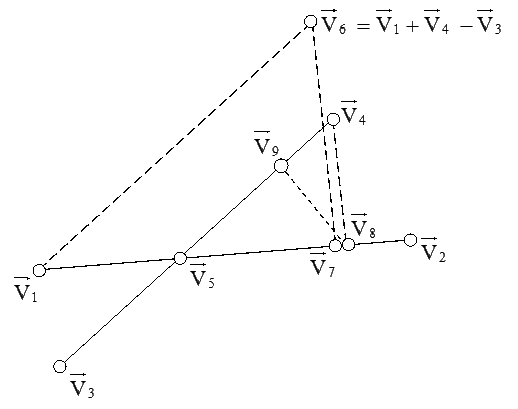
W celu wyznaczenia wektora V5 znajdującego się na przecięciu linii L1 z linią L2 należy obliczyć wektor V6 jak na rysunku 1 a następnie zrzutować ten wektor oraz wektor V4 prostopadle na linię L1. Otrzymane w ten sposób wektory wyznaczają dwa trójkąty prostokątne: pierwszy zbudowany jest na wektorach V1, V6, V7 a drugi na wektorach V5, V4, V8. Nie trudno zauważyć, że trójkąty te są trójkątami podobnymi dzięki czemu w prosty sposób określę odległość dzielącą wektor V4 od wektora V5. Ponieważ trójkąty podobne charakteryzuje pewna ważna dla nich cecha, otóż stosunek długości dwóch boków w jednym trójkącie jest równy stosunkowi odpowiednich dwóch boków trójkąta drugiego. Tak więc można a nawet trzeba ułożyć następujące równanie:
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_691.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
po odpowiednim przekształceniu otrzymuję wzór na upragnioną odległość dzielącą wektor V4 od wektora V5:
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_692.gif) | [2] |
Zapis wyrażenia w formacie TeX-a:
Potrzebny jest jeszcze jeden wektor uwzględniający kierunek i zwrot wektora V5-V4, w tym celu należy zrzutować wektor V8 na linię otrzymując w ten sposób wektor V9. Znając długość |V4-V5| można tak przeskalować wektor V9 - V4 aby otrzymać wektor V5-V4. Oczywiście operacja skalowania wektora wygląda następująco:
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_693.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
Do uzyskanego wektora V5-V4 należy jeszcze dodać wektor V4 aby otrzymać wektor V5.

Tytuł:
Algorytmy. Ilustrowany przewodnik
Autor:
Aditya Bhargava

Tytuł:
Algorytmy. Struktury danych i złożoność obliczeniowa
Autor:
Feliks Kurp

Tytuł:
Algorytmy w Pythonie. Techniki programowania dla praktyków
Autor:
Piotr Wróblewski

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Algorytmy kryptograficzne w Pythonie. Wprowadzenie
Autor:
Shannon W. Bray

Tytuł:
Algorytmy sztucznej inteligencji. Ilustrowany przewodnik
Autor:
Rishal Hurbans

Tytuł:
Algorytmy bez tajemnic
Autor:
Thomas H. Cormen

Tytuł:
Algorytmy dla bystrzaków
Autor:
John Paul Mueller, Luca Massaron

Tytuł:
Algorytmy Data Science. Siedmiodniowy przewodnik. Wydanie II
Autor:
David Natingga

Tytuł:
Algorytmy uczenia maszynowego. Zaawansowane techniki implementacji
Autor:
Giuseppe Bonaccorso
