Obliczenie punktów przecięcia okręgu z prostą
Stronę tą wyświetlono już: 4777 razy
Niech istnieją dwa wektory określające linię V1 i V2 oraz okrąg, dla którego dany jest punkt centralny VC i promień R (jak na rysunku 1). Konieczne jest następujące założenie: V1≠V2. Istnieje możliwość obliczenia wektorów V4 oraz V5 będących przecięciami prostej z tym okręgiem. Dowolna prosta może mieć z dowolnym okręgiem dwa punkty przecięcia (wektory V4 oraz V5 są różne), jeden punkt przecięcia (wektory V4 oraz V5 mają te same współrzędne) lub nie mieć punktów przecięcia. W celu obliczenia punktów przecięcia należy zrzutować prostopadle wektor VC na prostą opisaną wektorami V1 i V2 otrzymując w ten sposób wektor V3. Aby dowiedzieć się więcej o obliczeniach związanych z rzutowaniem prostopadłym punktu na prostą proszę o zapoznanie się z artykułem "Rzutowanie punktu prostopadle na prostą". Gdy spełniona jest nierówność |VC-V3|≤R wtedy okrąg ma jeden lub dwa punkty przecięcia z prostą i należy przystąpić do dalszych obliczeń współrzędnych tych punktów.
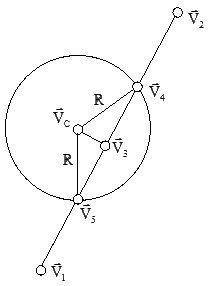
Na rysunku 1 pokazana jest interpretacja graficzna wcześniej wymienionych wektorów oraz linii i okręgu. Na tym rysunku można wyróżnić dwa trójkąty prostokątne, które są swoim lustrzanym odbiciem względem linii łączącej wektory VC oraz V3. Długość przeciwprostokątnej tych trójkątów jest znana i wynosi R, natomiast długość jednej z przyprostokątnych można wyznaczyć w następujący sposób:
Znając te dwie wartości można obliczyć długość wektora powstałego z różnicy wektorów V3 i V4 oraz V3 i V5 wykorzystując twierdzenie Pitagorasa:
Teraz należy obliczyć wektor pomocniczy Vp=V4-V3 wykorzystując fakt, że wektor ten jest równoległy do wektora V2-V1. W związku z powyższym wystarczy jedynie przeskalować uzyskany wektor V2-V1 tak aby jego długość wynosiła znaną już wartość L2. Operacja ta jest bardzo prosta i wygląda następująco:
A więc dzielę wektor V2-V1 przez jego długość uzyskując dzięki temu wektor o długości 1 i jednocześnie mnożę przez długość L2 uzyskując w ten sposób wektor o tejże długości. Mając wektor Vp można, a nawet trzeba obliczyć wektory V4 oraz V5 w następujący sposób:
Gdy okrąg ma z linią tylko jeden punkt przecięcia wektor Vp ma długość równą 0, w związku z czym punkty przecięcia V4, V5 oraz V3 mają te same współrzędne.

Tytuł:
Algorytmy. Ilustrowany przewodnik
Autor:
Aditya Bhargava

Tytuł:
Algorytmy. Struktury danych i złożoność obliczeniowa
Autor:
Feliks Kurp

Tytuł:
Algorytmy w Pythonie. Techniki programowania dla praktyków
Autor:
Piotr Wróblewski

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Algorytmy kryptograficzne w Pythonie. Wprowadzenie
Autor:
Shannon W. Bray

Tytuł:
Algorytmy sztucznej inteligencji. Ilustrowany przewodnik
Autor:
Rishal Hurbans

Tytuł:
Algorytmy bez tajemnic
Autor:
Thomas H. Cormen

Tytuł:
Algorytmy dla bystrzaków
Autor:
John Paul Mueller, Luca Massaron

Tytuł:
Algorytmy Data Science. Siedmiodniowy przewodnik. Wydanie II
Autor:
David Natingga

Tytuł:
Algorytmy uczenia maszynowego. Zaawansowane techniki implementacji
Autor:
Giuseppe Bonaccorso

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_694.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_695.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_696.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_697.gif)