Wyznaczanie punktu styczności do okręgu prostej przechodzącej przez dany punkt

Stronę tą wyświetlono już: 3635 razy

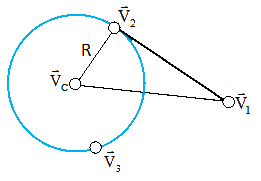
Dany jest okrąg O o promieniu R oraz środku w punkcie V_C oraz dowolny punkt V₁, z którego można poprowadzić linie styczne do tego okręgu gdy spełniona jest nierówność [1]. W przypadku, gdy nierówność [1] nie jest spełniona punkt V₁ znajduje się wewnątrz okręgu i nie jest możliwe poprowadzenie stycznych do okręgu O.

[1]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{V}_c-\vec{V}_1\right|>R

W celu wyznaczenia punktów styczności V₂ i V₃ konstrukcji geometrycznej z rysunku 31 należy wykorzystując stare dobre i poczciwe twierdzenie Pitagorasa obliczyć długość różnicy wektorów V₂ i V₁, wzór [2] wyznacza tę odległość.

[2]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{V}_2-\vec{V}_1\right|=\sqrt{R^2+\left|\vec{V}_C-\vec{V}_1\right|^2}

Nadszedł właściwy moment na wyznaczenie sinusa i kosinusa kąta leżącego pomiędzy wektorem V_C-V₂ a wektorem V_C-V₂. Do uzyskania tych wartości wykorzystane zostały stosunki odpowiednich długości boków trójkąta prostokątnego, jaki tworzą wektory V₂, V₁ oraz V_C (prostopadłość trójkąta wynika ze styczności wektora V₂ z okręgiem O). Zależności [3] oraz [4] umożliwiają wyliczenie sinusa i kosinusa kąta leżącego pomiędzy wektorem V_C-V₂ a wektorem V_C-V₂.

[3]

Zapis wyrażenia w formacie TeX-a:

sin(\alpha)=\frac{\left|\vec{V}_2-\vec{V}_1\right|}{\left|\vec{V}_C-\vec{V}_1\right|}

[4]

Zapis wyrażenia w formacie TeX-a:

\cos(\alpha)=\frac{R}{\left|\vec{V}_C-\vec{V}_1\right|}

Teraz można przystąpić do obliczenia wektora pomocniczego V_p w następujący sposób:

[5]

Zapis wyrażenia w formacie TeX-a:

\vec{V}_p=\frac{\vec{V}_1-\vec{V}_C}{\left|\vec{V}_1-\vec{V}_C\right|}\cdot R

Teraz należy obrócić wektor pomocniczy V_p wykorzystując w tym celu wcześniej obliczone wartości sin(α) oraz cos(α) i dodać wektor przesunięcia V_C

[6]

Zapis wyrażenia w formacie TeX-a:

V_2.x=V_p.x\cdot \cos(\alpha)-V_p.y\cdot \sin(\alpha)+V_{C}.x

[7]

Zapis wyrażenia w formacie TeX-a:

V_2.y=V_p.x\cdot \sin(\alpha)+V_p.y\cdot \cos(\alpha)+V_{C}.y

[8]

Zapis wyrażenia w formacie TeX-a:

V_3.x=V_p.x\cdot \cos(\alpha)+V_p.y\cdot \sin(\alpha)+V_{C}.x

[9]

Zapis wyrażenia w formacie TeX-a:

V_3.y= V_p.y\cdot \cos(\alpha)-V_p.x\cdot \sin(\alpha)+V_{C}.y

Tytuł:

Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie

Autor:

Ryan T. White, Archana Tikayat Ray

Tytuł:

Algorytmy kryptograficzne w Pythonie. Wprowadzenie

Autor:

Shannon W. Bray

Tytuł:

Algorytmy sztucznej inteligencji. Ilustrowany przewodnik

Autor:

Rishal Hurbans

Tytuł:

Algorytmy bez tajemnic

Autor:

Thomas H. Cormen

Tytuł:

Algorytmy dla bystrzaków

Autor:

John Paul Mueller, Luca Massaron

Tytuł:

Algorytmy Data Science. Siedmiodniowy przewodnik. Wydanie II

Autor:

David Natingga

Tytuł:

Algorytmy uczenia maszynowego. Zaawansowane techniki implementacji

Autor:

Giuseppe Bonaccorso

Tytuł:

Struktury danych i algorytmy w języku Java. Przewodnik dla początkujących

Autor:

James Cutajar

Tytuł:

C++. Struktury danych i algorytmy

Autor:

Wisnu Anggoro

Tytuł:

Struktury danych i algorytmy w języku C#. Projektowanie efektywnych aplikacji

Autor:

Marcin Jamro

Załączniki:

Komentarze