Ułamki łańcuchowe

Stronę tą wyświetlono już: 12013 razy

Ułamkiem łańcuchowym nazywane jest wyrażenie zapisane w postaci [1]. Za pomocą ułamków łańcuchowych możliwe jest zapisanie każdej liczby rzeczywistej, przy czym dla liczby wymiernej ułamek jest skończony, natomiast dla niewymiernej nieskończony.

[1]

Zapis wyrażenia w formacie TeX-a:

a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+_{\ddots _{\cfrac{1}{a_n}}}}}

Zapis [1] ze względu na wygodę często zastępuje się następującym zapisem w notacji poziomej :

[2]

Zapis wyrażenia w formacie TeX-a:

[a_0, a_1, a_2,\cdots,a_n]

Istnieje również zapis ułamka łańcuchowego w notacji Pringsheima, której postać jest następująca:

[3]

Zapis wyrażenia w formacie TeX-a:

a_0 + \frac{1 \mid}{\mid a_1} + \frac{1 \mid}{\mid a_2} + \frac{1 \mid}{\mid a_3} + \cdots+\frac{1 \mid}{\mid a_n}

Dla liczby 125.23236 ułamek łańcuchowy przyjmuje następującą postać:

[4]

Zapis wyrażenia w formacie TeX-a:

125+\frac{1}{4+\cfrac{1}{3+\cfrac{1}{3+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{14+\cfrac{1}{2}}}}}}}}}

Zapis [4] w notacji poziomej:

[5]

Zapis wyrażenia w formacie TeX-a:

[125, 4, 3, 3, 2, 2, 2, 1, 14, 2]

i w notacji Pringsheima:

[6]

Zapis wyrażenia w formacie TeX-a:

125 + \frac{1\mid}{mid4}+ \frac{1\mid}{\mid 3}+ \frac{1\mid}{\mid 3} + \frac{1\mid}{\mid 2}+ \frac{1\mid}{mid 2}+ \frac{1\mid}{\mid 2} + \frac{1\mid}{\mid 1}+ \frac{1\mid}{\mid 14}+ \\frac{1mid}{\mid 2}

Obliczenie poszczególnych elementów ciągu a_n składają się z podziału ułamka podstawowego np. 125.23236 na część całkowitą a₀=125 i resztę r = 0.23236, na kolejnych etapach oblicza się odwrotność reszty r i dzieli się w ten sposób uzyskaną wartość ponownie na część całkowitą a_n i resztę r. Dla rozpatrywanego przypadku kolejność działań będzie następująca:

Liczby niewymierne

Również liczby niewymierne można zapisać w postaci ułamka łańcuchowego, o nieskończonej liczbie elementów ciągu. Najlepszym przykładem jest pierwiastek z 2, który można rozpisać na część całkowitą a i resztę r w sposób następujący:

[7]

Zapis wyrażenia w formacie TeX-a:

\sqrt{2}=1\+sqrt{2}-1

gdzie:

1 - część całkowita a
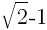- reszta r

Teraz równanie [7] można rozpisać w następujący sposób:

[8]

Zapis wyrażenia w formacie TeX-a:

\sqrt{2}=1+\sqrt{2}-1=1+\frac{1}{\cfrac{1}{\sqrt2-1}}=1+\frac{1}{\cfrac{1}{\sqrt2-1}\cdot \cfrac{\sqrt2+1}{\sqrt2+1}}=1+\frac{1}{\sqrt{2}+1}=1+\frac{1}{1+\sqrt{2}-1+1}=1+\frac{1}{2+\sqrt2-1}=\frac{1}{2+\cfrac{1}{\cfrac{1}{\sqrt2-1}}}=1+\frac{1}{2+\cfrac{1}{2+\sqrt2-1}}=1+\frac{1}{2+\cfrac{1}{2+_{\ddots}}}

W podobny sposób można postąpić z pierwiastkiem z 3, dzieląc go na część całkowitą a i resztę r, w następujący sposób:

[9]

Zapis wyrażenia w formacie TeX-a:

\sqrt{3}=1+\sqrt{3}-1

Rozpiszmy więc po raz kolejny równanie [9] w następujący sposób:

[10]

Zapis wyrażenia w formacie TeX-a:

\sqrt{3}=1+\sqrt{3}-1=1+\frac{1}{\cfrac{1}{\sqrt3-1}\cdot\cfrac{\sqrt3+1}{\sqrt3+1}}=1+\frac{1}{\cfrac{\sqrt3+1}{2}}=1+\frac{1}{\cfrac{2+\sqrt3+1}{2}}=1+\frac{1}{1+\cfrac{\sqrt3-1}{2}}=1+\frac{1}{\cfrac{2+\sqrt3+1}{2}}=1+\frac{1}{1+\cfrac{1}{\cfrac{2}{\sqrt3-1}\cdot\cfrac{\sqrt3+1}{\sqrt3+1}}}=1+\frac{1}{1+\cfrac{1}{\sqrt3+1}}=1+\frac{1}{1+\cfrac{1}{2+\sqrt3-1}}=1+\frac{1}{1+\cfrac{1}{2+\cfrac{1}{\cfrac{1}{\sqrt3-1}}}}=1+\frac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{2+_{\ddots}}}}}

Możliwe jest uzyskanie nieco ładniejszego zapisu ułamka łańcuchowego, poprzez wprowadzenie zmiennej pomocniczej r, której wartość jest następująca:

[11]

Zapis wyrażenia w formacie TeX-a:

r=\sqrt3-1

Zależność [11], można rozpisać w następujący sposób:

[12]

Zapis wyrażenia w formacie TeX-a:

(r+1)^2=3\Rightarrow r^2+2\cdot r+1=3\Rightarrow r\cdot(r+2)=2\Rightarrow r=\frac{2}{r+2}

Podstawiając do równania [9] i rozpisując uzyskujemy następujący wynik:

[13]

Zapis wyrażenia w formacie TeX-a:

\sqrt3=1+r=1+\frac{2}{2+r}=1+\frac{2}{2+\cfrac{2}{2+r}}=1+\frac{2}{2+\cfrac{2}{2+_\ddots}}

Stała π w zapisie łańcuchowym Eulera

[14]

Zapis wyrażenia w formacie TeX-a:

\pi=2+\cfrac{4}{3+\cfrac{1\cdot 3}{4+\cfrac{3\cdot 5}{4+\cfrac{5\cdot 7}{4+_\ddots}}}}

Stała Eulera e w zapisie łańcuchowym

[15]

Zapis wyrażenia w formacie TeX-a:

e= 2+\frac{1}{1+\cfrac{1}{2+\cfrac{2}{3+\cfrac{3}{\ddots}}}}

Ułamki łańcuchowe w funkcjach trygonometrycznych

[16]

Zapis wyrażenia w formacie TeX-a:

\sin x=\cfrac{x}{1+cfrac{x^2}{(2\cdot 3-x^2)+\cfrac{2\cdot 3 x^2}{(4\cdot 5-x^2)+\cfrac{4\cdot 5 x^2}{(6\cdot 7-x^2)+_\ddots}}}}

[17]

Zapis wyrażenia w formacie TeX-a:

tg x=\cfrac{x}{1-\cfrac{x^2}{3-\cfrac{x^2}{5-\cfrac{x^2}{7-_\ddots}}}}=\cfrac{1}{\cfrac{1}{x}-\cfrac{1}{\cfrac{3}{x}-\cfrac{1}{\cfrac{5}{x}-\cfrac{1}{\cfrac{7}{x}-_\ddots}}}}