Obliczenia układów dynamicznych metodą równoważności energii i pracy
Stronę tą wyświetlono już: 7250 razy
Obliczyć przyspieszenie ac krążka toczącego się bez poślizgu po poziomej płaszczyźnie połączonego za pośrednictwem nieważkiego i nierozciągliwego cięgna z krążkiem, do którego przyłożony został moment obrotowy M będący jedynym czynnikiem wywołujący ruch układu.
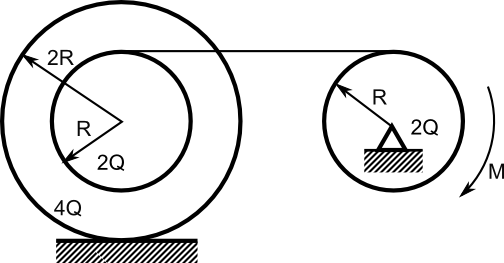
Dane:
![R[m]; Q[N]; M[Nm]](rownania/w_579.gif)
Rozwiązanie:
Na rysunku 1 zaznaczone zostały jedynie podstawowe informacje, bez oznaczenia wektorów liniowej prędkości chwilowej oraz kątowej, a także założonych przesunięć układu niezbędnymi do ułożenia równania równowagi pracy L i energii E. Innymi słowy trzeba zrobić nowy rysunek z wszystkimi potrzebnymi oznaczeniami.
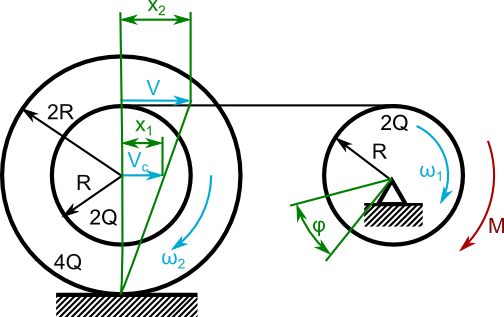
Zgodnie z wzorem [1] z strony Mechanika techniczna → Dynamika → Zasada równowagi pracy i energii oraz zgodnie z opisywanymi tam zasadami, jedynym czynnikiem wykonującym pracę na układzie jest w tym przypadku moment obrotowy M. W związku z czym prawa strona wcześniej wspomnianego już równania [1] przyjmie następującą wartość:
gdzie φ jest zadanym przemieszczeniem spowodowanym przez moment obrotowy M. Jest to wielkość nieznana, która na końcu zredukuje się więc nie ma strachu w naszym fachu.
Z wspomnianym już przed chwilą przemieszczeniem kątowym φ związane są bezwzględnie inne przemieszczenie zaznaczone na rysunku 2 przez x1 i x2. Tak więc, aby mieć to już za sobą zapiszę tutaj zależności przemieszczeń x1, x2 od przemieszczenia kątowego φ.
Przemieszczenie x2 jest równe długości łuku, którego kąt jest równy φ a promień wynosi R, a więc podstawowa szkoła się kłania:
A co z przemieszczeniem liniowym x2? Tutaj chyba nie pójdzie tak łatwo? Ależ pójdzie, pójdzie bo przecież znamy starą dobrą zasadę konstrukcji chwilowego środka obrotu opisaną przeze mnie na stronie Mechanika techniczna → Dynamika → Konstrukcja chwilowego środka obrotu. Nie tracąc już więc czasu i w przebiegły skądinąd sposób wykorzystam w perfidny sposób wcześniej wspomnianą zasadę określając tym samym zależność przemieszczenia liniowego x1 od przemieszczenia liniowego x2 w następujący sposób:
Ponieważ szukam zależności x1 od φ, a nie od x2, więc do równania końcowego [3] muszę podstawić równanie 2 uzyskując tym samym szukaną zależność:
Nadszedł czas aby dorwać się do zależności kinetycznych układu. Ponieważ mam za zadanie wyznaczyć przyspieszenie kątowe ac układu, a jak się na końcu okaże do tego będzie trzeba wyznaczyć chwilową prędkość liniową Vc, więc wszystkie niewiadome związane z ruchem należy uzależnić od Vc. Zacznę więc od zależności prędkości liniowej V od Vc wykorzystując po raz kolejny starą dobrą zasadę konstrukcji chwilowego środka obrotu (tak jak już wcześniej było to robione w tym zadaniu):
Zależność prędkości kątowej ω2 od prędkości Vc:
Kolej na zależność ω1 od x1:
W zależności [7] podstawiłem od razu za V zależność [6] zmniejszając tym samym męczarnie rozpisywanie tej zależności w dwóch częściach.
Dobra, będzie tego, czas zabrać się za prawą stronę równania [1] ze strony Mechanika techniczna → Dynamika → Konstrukcja chwilowego środka obrotu. Czas zapisać energię kinetyczną całego układu.
Energia kinetyczna krążka znajdującego się po lewej stronie rysunku 2 jest równa sumie energii ruchu prostoliniowego oraz energii obrotu względem środka ciężkości. A więc suma tych energii jest równa:
Teraz rozpisać należy wzór na energię kinetyczną obracającego się krążka po prawej stronie rysunku 2 w następujący sposób:
Albowiem powiedzieliśmy już sobie, że energia kinetyczna E wszystkich elementów rozpatrywanego układu musi być równa pracy L na nim wykonanej, więc niezwłocznie takie równanie musi być zapisane:
W uzyskanym powyżej równaniu [10] znajdują się aż cztery niewiadome, a są to proszę Państwa: Vc; ω1; ω2 i φ. Należy z tego wszystkiego wyznaczyć Vc2, przekształcając i podstawiając za ω1 i ω2 rozpisane wcześniej relacje kinetyczne. A φ nie trzeba się przejmować, bo się z nim rozprawimy na końcu.
Ponieważ nie jestem niańką do opieki nad dziećmi więc nie będę rozpisywał całego procesu podstawiania i upraszczania, podając tym samym wzór [10] po podstawieniu, uproszczeniu i przekształceniu:
Koniec zadania jest już bliski, albowiem wystarczy sobie przypomnieć ze szkoły średniej, że siła P jest równa iloczynowi przyspieszenia a i masy m rozpatrywanego ciała, zaś siła P razy przemieszczenie s to nic innego jak praca L, zaś praca musi być równa w tym przypadku energii kinetycznej danego układu.
Tak więc, w przypadku tego zadania praca L samego krążka znajdującego się po lewej stronie rysunku 2 związanego z przemieszczeniem liniowym jest równa energii tegoż przemieszczenia. Czyli:
Do zależności [12] należy za Vc2 podstawić wyrażenie [11] a za x1 zależność [4], uzyskując koniec, końców wzór na upragnioną wartość przyspieszenia ac:
Możliwe, że zauważyliście iż uzyskany wynik dziwnym zbiegiem okoliczności jest taki sam, jak ten, który został uzyskany w zadaniu 1 ze strony Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona. Dziwna sprawa, to samo zadanie policzone inną metodą i wyszło to samo? Witamy w świecie nauk ścisłych.
Obliczyć przyśpieszenie ac krążka o masie m zawieszonego na nieważkim i nierozciągliwym cięgnie.

Dane:
![r[m];m[kg]](rownania/w_588.gif)
Rozwiązanie:
Przed przystąpieniem do rozwiązania zadania, uzupełnić należy najpierw oznaczenia na rysunku 3 tak jak to zostało wykonane na rysunku 4.
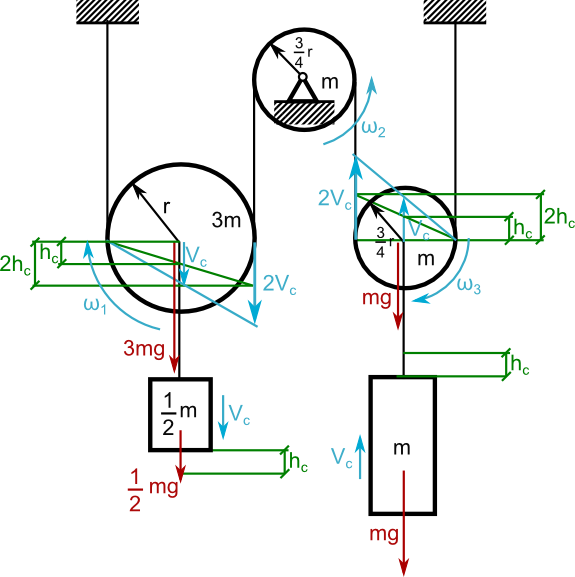
Jak widać, na rysunku 4 naniesione już zostały podstawowe zależności przemieszczeń liniowych w zależności od hc oraz liniowych prędkości w zależności od Vc co ułatwi rozpisanie równania energii kinetycznej E układu:
Po uproszczeniu i uporządkowaniu powyższe równanie przyjmuje następującą postać:
Konieczne jest rozpisanie zależności kinetycznych by w bezwzględny sposób móc pozbyć się z równania [15] niewiadomych ω1, ω2 i ω3 uzależniając je całkowicie od niewiadomej Vc.
Najpierw ω1 od Vc:
a następnie ω2:
Na koniec z zależności kinetycznych została już tylko prędkość kątowa ω3:
Pozostało już podstawić zależności [16], [17] i [18] do równania [15] otrzymując tym samym uproszczony wzór na energię kinetyczną całego układu:
Nadszedł najwyższy czas na wyznaczenie pracy sił czynnych na drodze hc, którymi są oczywiście siły ciężkości ciężarków. Równanie pracy L1-2 przyjmie więc następującą postać:
Zgodnie z zasadą równoważności pracy L i energii E przyrównać należy energię kinetyczną całego układu [19] do pracy na nim wykonanej przez siły czynne [20]:
Po przekształceniu równania [21] uzyskuje się wzór na Vc2:
Pozostało tylko rozpisać równanie, którego lewą stronę będzie stanowił wzór na pracę L podukładu związanego z przyspieszeniem liniowym ac zaś prawą wzór na energię kinetyczną E tegoż podukładu:
Za Vc2 do równania [23] podstawić należy zależność [22] otrzymując tym samym końcowy wzór na przyspieszenie liniowe ac:
Po raz kolejny dziwnym zbiegiem okoliczności wynik jest taki sam, jak ten, który został uzyskany w zadaniu 2 ze strony Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona.
Obliczyć przyśpieszenie ac krążka o ciężarze 4Q zawieszonego na nieważkim i nierozciągliwym cięgnie.

Dane:
![r[m];Q[N]](rownania/w_604.gif)
Rozwiązanie:
Tradycyjnie od uzupełnienia rysunku zacząć trzeba.
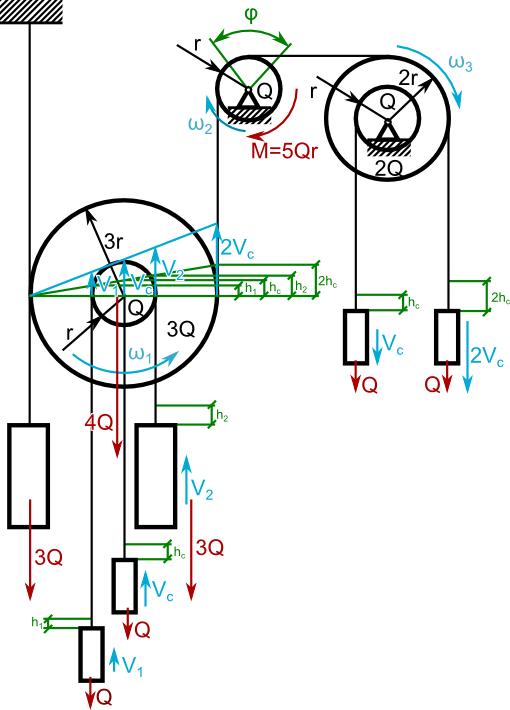
Czas napisać równanie energetyczne E rozpatrywanego układu w następujący sposób:
Po uproszczeniu i uporządkowaniu równania [25] otrzymuje się taki oto śliczny wzór:
Ponieważ należy wyznaczyć Vc2 więc w bezwzględny sposób należy pozbyć się niewiadomych V1, V2, ω1; ω2 oraz (jakże by inaczej) ω3 uzależniając te niewiadome od Vc. Tak więc chciał nie chciał trzeba zakasać rękawy i napisać zależności kinetyczne.
Relacja kinetyczna dla ω1:
Relacja kinetyczna dla ω2:
Relacja kinetyczna dla ω3:
Relacja kinetyczna dla V1:
Relacja kinetyczna dla V2:
Pozostało już podstawić do równania [26] zależności od 27 do 31 a otrzymane równanie uprościć uzyskując takową postać jego:
Czas zabrać się za ułożenie równania pracy L czynników wywołujących ruch układu:
Chciał nie chciał, radził, nie radził trza zależności przemieszczeń wyprowadzić. Zależność przemieszczenia h1 od hc:
Zależność przemieszczenia h2 od hc:
Zależność przemieszczenia kątowego φ od hc:
Podstawienie do równania [34] zależności od 34 do 36 z uproszczeniem:
W powyższej zależności podstawiono za M wartość podaną w zadaniu, czyli 5·Q·r.
Pozostało już tylko przyrównanie całkowitej energii kinetycznej E układu (zależność [32]) do pracy L na nim wykonanej (zależność [37]):
Praca krążka związanego z prędkością kątową ac musi być równa energii kinetycznej tego układu w danej chwili, a więc następujące równanie należy zapisać:
Ostatnie podstawienie do równania [39] za Vc2 zależności [38]:
Po raz kolejny dziwnym zrządzeniem losu otrzymany wynik jest taki sam, jak ten z zadania 3 umieszczonego na stronie Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona.
Obliczyć przyśpieszenie a ciężarka o masie 2m położonego na płaskiej poziomej płaszczyźnie. W układzie należy pominąć tarcie ciężarków o podłoże oraz masę cięgna.

Dane:
![R[m];m[kg]](rownania/w_627.gif)
α=30°
Rozwiązanie:
Naniesienie dodatkowych oznaczeń na rysunku 8.
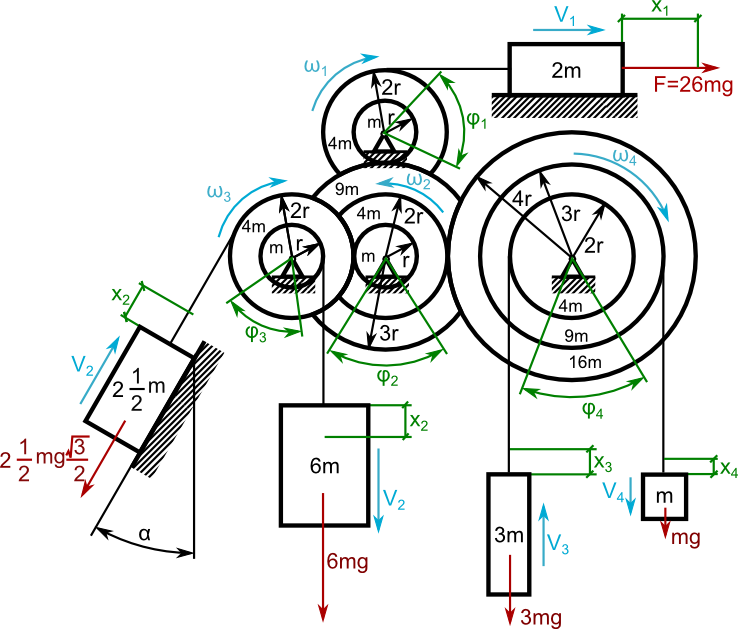
Równanie energii kinetycznej całego układu:
Jakże piękne równanie [41] wypadałoby uporządkować co nieco w następujący sposób, bo sposoby:
Nie tracąc czasu czym prędzej rozpisać należy zależności kinetyczne, by po raz kolejny pozbyć się niewiadomych ω1, ω2, ω3, ω4, V2, V3 oraz V4 z równania [42] poprzez uzależnienie ich od niewiadomej V1.
Zależność kinetyczna ω1 od V1:
Zależność kinetyczna ω2 od V1:
Zależność kinetyczna ω3 od V1:
Zależność kinetyczna ω3 od V1:
Zależność kinetyczna V2 od V1:
Zależność kinetyczna V3 od V1:
Zależność kinetyczna V4 od V1:
Po podstawieniu do równania [42] zależności kinetycznych od [43] do [49] i uproszczeniu powinno się uzyskać następujący wynik:
Najwyższa pora i czas na rozpisanie równania pracy L wykonanej przez siły czynne na układzie:
Z równania [51] trzeba się pozbyć niewiadomych x2, x3 oraz x4 uzależniając je od niewiadomej x1.
Zależność przemieszczenia φ1 od przemieszczenia x1:
Zależność przemieszczenia φ2 od przemieszczenia x1:
Zależność przemieszczenia φ3 od przemieszczenia x1:
Zależność przemieszczenia x2 od przemieszczenia x1:
Zależność przemieszczenia φ4 od przemieszczenia x1:
Zależność przemieszczenia x3 od przemieszczenia x1:
Zależność przemieszczenia x4 od przemieszczenia x1:
Podstawiając do równania [51] zależności [55], [57] i [58] oraz upraszczając je otrzymuje się następującą końcową jego postać:
Przyrównanie pracy L opisanej równaniem [59] i energii kinetycznej E całego układu zapisanej w równaniu [50]:
Wyznaczyć trzeba V12 w sposób następujący:
Równanie pracy L układu związanego z przyspieszeniem a i energii kinetycznej E tegoż układu:
Przekształcając powyższe równanie w końcu uzyskuje się następujący upragniony wzór na przyspieszenie a:
I znów dziwnym zrządzeniem losu otrzymany wynik jest taki sam, jak ten z zadania 4 umieszczonego na stronie Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona.
Obliczyć przyśpieszenie a krążka toczącego się bez poślizgu po równi pochyłej.

Dane:
![R[m];m[kg]](rownania/w_627.gif)
Rozwiązanie:
Uzupełnienie oznaczeń.
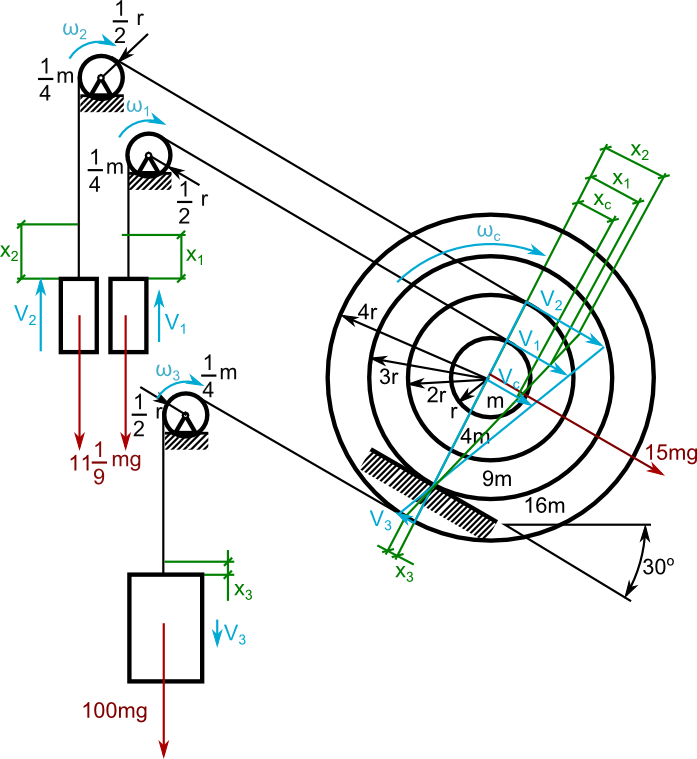
Jak tradycja nakazuje tu energię rozpisuję:
i upraszczam, redukuję, taką postać otrzymuję:
Relacje kinetyczne rozpisuję:
Znów podstawić, zredukować:
Na pracę sił czynnych równanie rozpisuję:
i zależności przemieszczeń odnajduję:
Znów podstawiam, redukuję, taką postać pracy otrzymuję:
Pracę i energię do siebie przyrównuję i takie oto równanie otrzymuję:
Po przekształceniu otrzymuję:
Pracę i energię układu z ac związanego do siebie przyrównuję:
Przekształcam, redukuję i ac otrzymuję:
Drogi czytelniku, jeżeli nadal rozwiązywać tych zadań nie umiesz: "then my old Jedi friend I cannot help You anymore"

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1809.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1810.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1811.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_1812.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1813.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1814.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_1815.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_1816.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_1817.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_1818.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_1819.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_1820.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_1821.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_1822.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_1823.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_1824.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_1825.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_1826.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_1827.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_1828.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_1829.gif)
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_1830.gif)
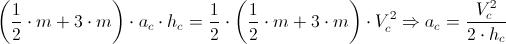
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_1832.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_1833.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_1834.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_1835.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_1836.gif)
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_1837.gif)
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_1838.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_1839.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_1840.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_1841.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_1842.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_1843.gif)
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_1844.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_1845.gif)
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_1846.gif)
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_1847.gif)
![a_c=frac{8}{143}cdot gleft[frac{m}{s^2}right]](https://obliczeniowo.com.pl/rownania/w_1848.gif)
![Równanie [41]](https://obliczeniowo.com.pl/rownania/w_1849.gif)
![Równanie [42]](https://obliczeniowo.com.pl/rownania/w_1850.gif)
![Równanie [43]](https://obliczeniowo.com.pl/rownania/w_1851.gif)
![Równanie [44]](https://obliczeniowo.com.pl/rownania/w_1852.gif)
![Równanie [45]](https://obliczeniowo.com.pl/rownania/w_1853.gif)
![Równanie [46]](https://obliczeniowo.com.pl/rownania/w_1854.gif)
![Równanie [47]](https://obliczeniowo.com.pl/rownania/w_1855.gif)
![Równanie [48]](https://obliczeniowo.com.pl/rownania/w_1856.gif)
![Równanie [49]](https://obliczeniowo.com.pl/rownania/w_1857.gif)
![Równanie [50]](https://obliczeniowo.com.pl/rownania/w_1858.gif)
![Równanie [51]](https://obliczeniowo.com.pl/rownania/w_1859.gif)
![Równanie [52]](https://obliczeniowo.com.pl/rownania/w_1860.gif)
![Równanie [53]](https://obliczeniowo.com.pl/rownania/w_1861.gif)
![Równanie [54]](https://obliczeniowo.com.pl/rownania/w_1862.gif)
![Równanie [55]](https://obliczeniowo.com.pl/rownania/w_1863.gif)
![Równanie [56]](https://obliczeniowo.com.pl/rownania/w_1864.gif)
![Równanie [57]](https://obliczeniowo.com.pl/rownania/w_1865.gif)
![Równanie [58]](https://obliczeniowo.com.pl/rownania/w_1866.gif)
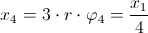
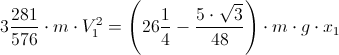
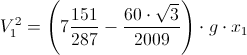
![Równanie [62]](https://obliczeniowo.com.pl/rownania/w_1870.gif)
![a=left(3frac{219}{287}-frac{30cdotsqrt{3}}{2009}right)cdot gapprox 3,7372cdot gleft[frac{m}{s^2}right]](https://obliczeniowo.com.pl/rownania/w_1871.gif)
![Równanie [64]](https://obliczeniowo.com.pl/rownania/w_1872.gif)
![Równanie [65]](https://obliczeniowo.com.pl/rownania/w_1873.gif)
![Równanie [66]](https://obliczeniowo.com.pl/rownania/w_1874.gif)
![Równanie [67]](https://obliczeniowo.com.pl/rownania/w_1875.gif)
![Równanie [68]](https://obliczeniowo.com.pl/rownania/w_1876.gif)
![Równanie [69]](https://obliczeniowo.com.pl/rownania/w_1877.gif)
![Równanie [70]](https://obliczeniowo.com.pl/rownania/w_1878.gif)
![Równanie [71]](https://obliczeniowo.com.pl/rownania/w_1879.gif)
![Równanie [72]](https://obliczeniowo.com.pl/rownania/w_1880.gif)
![Równanie [73]](https://obliczeniowo.com.pl/rownania/w_1881.gif)
![Równanie [74]](https://obliczeniowo.com.pl/rownania/w_1882.gif)
![Równanie [75]](https://obliczeniowo.com.pl/rownania/w_1883.gif)
![Równanie [76]](https://obliczeniowo.com.pl/rownania/w_1884.gif)
![Równanie [77]](https://obliczeniowo.com.pl/rownania/w_1885.gif)
![Równanie [78]](https://obliczeniowo.com.pl/rownania/w_1886.gif)
![Równanie [79]](https://obliczeniowo.com.pl/rownania/w_1887.gif)
![Równanie [80]](https://obliczeniowo.com.pl/rownania/w_1888.gif)
![Równanie [81]](https://obliczeniowo.com.pl/rownania/w_1889.gif)
![a_c=frac{4860}{36281}cdot gleft[frac{m}{s^2}right]](https://obliczeniowo.com.pl/rownania/w_1890.gif)