Ogólne równanie dynamiki d'Alamberte'a Lagrange'a
Stronę tą wyświetlono już: 3973 razy
Najwyższy czas zająć się siłami bezwładności zwanymi siłami d'Alamberte'a. W tym jakże zacnym celu rozpatrzmy najprostszy układ w postaci ciała o masie m, które porusza się z przyspieszeniem a.

Siła bezwładności F będzie miała wektor przeciwny do kierunku ruchu, a więc będzie ona równa:
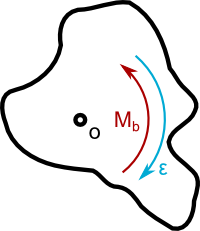
Podobnie sytuacja ma się w przypadku momentu bezwładności d'Alamberte'a Mb, który jest równy iloczynowi przyspieszenia kątowego ε i masowego odśrodkowego współczynnika bezwładności Io.
Zapoznajmy się z zasadą prac przygotowawczych, która jak się okaże jest w bezpośredni sposób związana z ogólnym równaniem dynamiki d'aLagrange'a. Suma prac wykonanych przez wszystkie siły czynne i siły bezwładności na zadanym przemieszczeniu przygotowawczym musi być równa zeru, co zapiszę jeszcze dla świętego spokoju za pomocą następującego wzoru ogólnego:
Powyższą zasada umożliwia rozwiązywanie zadań takich, jak na stronach: Mechanika techniczna → Dynamika → Obliczenia układów dynamicznych metodą równoważności energii i pracy oraz Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona, ale to już jest temat na inną okazję.

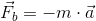
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2320.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2321.gif)