Stronę tą wyświetlono już: 13827 razy

Dla bryły z rysunku 1 wyznaczyć płaszczyznę jej przecięcia płaszczyzną ABC.

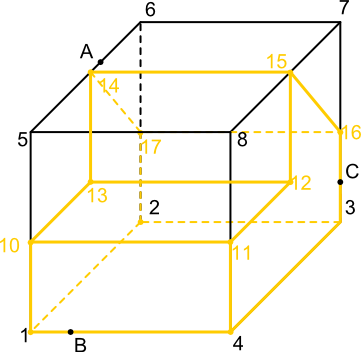
Tak się jakoś składa, że specjalnie wybrałem sobie takie punkty płaszczyzny ABC, które były użyte w zadaniu na stronie tutaj, w związku z czym pominę tutaj serię niezbędnych do wykonania czynności, które były na owej stronie omówione dość dokładnie.

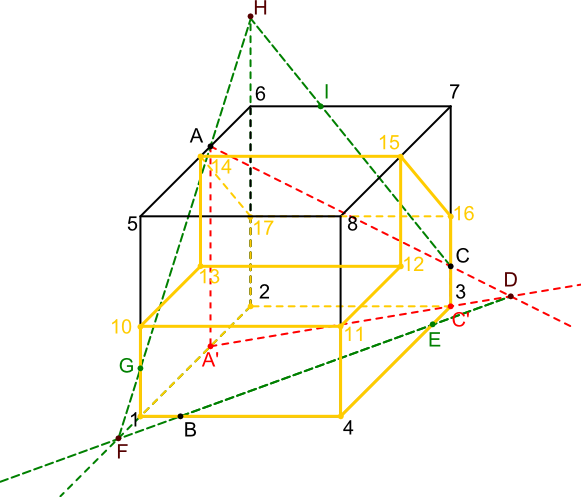
Jak widać na rysunku 2 niektóre linie przecięcia prostopadłościanu z płaszczyzną ABC stanowi również przecięcie naszej bryły. Tak jest chociażby z odcinkiem BE leżącym w płaszczyźnie podstawy. Nie trudno jest też zauważyć, że niektóre proste leżą częściowo na płaszczyznach bocznych bryły. Dotyczy to płaszczyzn 1-2-17-14-13-10; 2-3-16-17 oraz 3-4-11-12-15-16, tym samym można poprowadzić już pogrubione linie płaszczyzny ścięcia bryły jak na rysunku 3.

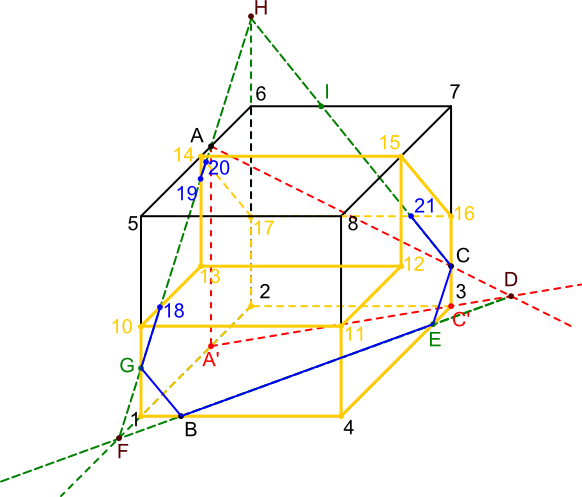
Jak widać na rysunku 3 uzyskano sporo linii przecięcia bryły z płaszczyzną ABC, co z kolei pozwoliło na uzyskanie nowych punktów. Dwa z tych punktów leżą na płaszczyźnie 14-15-16-17, a więc można je śmiało połączyć prostą. Niestety z wyznaczeniem dodatkowego punktu na płaszczyźnie 12-13-14-15 nie będzie już takie łatwe, ale nie ma strachu w naszym fachu. Wystarczy uświadomić sobie, ze odcinek 14-15 tejże płaszczyzny leży na płaszczyźnie 5-6-7-8 a na tejże płaszczyźnie z kolei leżą aż dwa punkty: A oraz I. Poprowadzić należy czym prędzej linię przez owe punkty a następnie przedłużyć odcinek 14-15 aż do przecięcia się z ową linią. Otrzymany w ten jakże przebiegły sposób punkt J leży na płaszczyźnie ABC oraz na płaszczyźnie 12-13-14-15, na której znaleziony został już wcześniej punkt 20. Wystarczy pociągnąć prostą przez punkty J i 20 aż do przecięcia z krawędzią 12-13 płaszczyzny 12-13-14-15, aby znaleźć brakujący punkt 22 a więc tym samym ostatnie krawędzie płaszczyzny przecięcia.

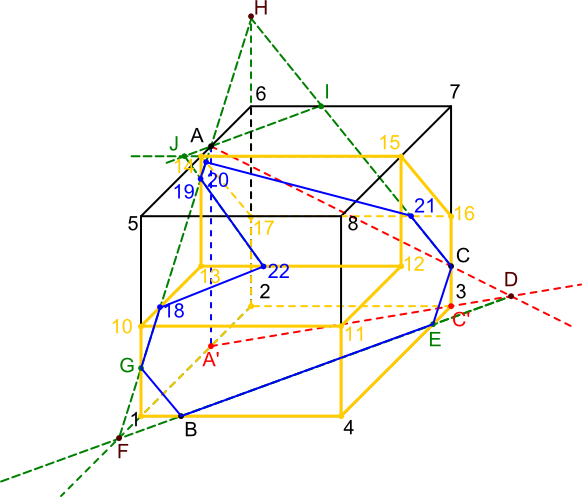
Teraz, gdy wszystko jest już jasne pozbądźmy się niepotrzebnych oznaczeń i linii pozostawiając jedynie ściętą część bryły, która nie zasłania płaszczyzny ścięcia.