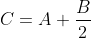Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 20702 razy

Pomiar pośredni wymaga często przeprowadzenia kilku pomiarów oraz związanych z nimi dodatkowymi obliczeniami.

Typowym i dość częstym przypadkiem takich pomiarów jest określenie położenia środka otworu jak na rysunku 1, gdzie w celu wyznaczenia wymiaru C konieczne jest zmierzenie wymiaru A oraz B.

Przykład pomiaru pośredniego w przypadku określania położenia odległości środka otworu od jednej z krawędzi przedmiotu.
Rys. 1
Przykład pomiaru pośredniego w przypadku określania położenia odległości środka otworu od jednej z krawędzi przedmiotu.

Oczywistym jest, że wymiar C wyznacza następujący wzór:

C=A+frac{B}{2} [1]

Zapis wyrażenia w formacie TeX-a:

C=A+\frac{B}{2}

Kolejnym przykładem jest pomiar zbieżności stożka wewnętrznego za pomocą kulek pomiarowych o znanej średnicy D1, D2. Sposób pomiaru pokazany został na rysunku 2 i polega na określeniu wysokości h1, h2.

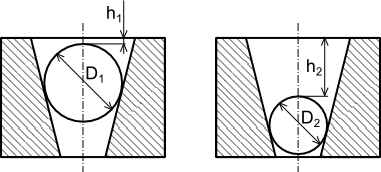
Przykład pomiaru pośredniego w przypadku określania kąta zbieżności stożka wewnętrznego.
Rys. 2
Przykład pomiaru pośredniego w przypadku określania kąta zbieżności stożka wewnętrznego.

W tym przypadku wzór obliczeniowy będzie nieco ciekawszy od poprzedniego przypadku i przyjmuje on następującą postać:

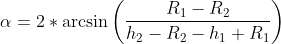alpha=2*arcsin left(frac{R_{1}-R_{2}}{h_{2}-R_{2}-h_{1}+R_{1}}right) [2]

Zapis wyrażenia w formacie TeX-a:

\alpha=2*\arcsin \left(\frac{R_{1}-R_{2}}{h_{2}-R_{2}-h_{1}+R_{1}}\right)

Oczywiście we wzorze [2] użyto promieni kulek pomiarowych a na rysunku 2 zaznaczono ich średnice, jednakże mam taką skromną nadzieję, że każdy z was potrafi obliczyć promień znając średnicę.