Prawdopodobieństwo całkowite
Stronę tą wyświetlono już: 13311 razy
Z prawdopodobieństwem całkowitym mamy do czynienia np. 1) przy losowaniu kuli z kilku urn; 2) przy losowaniu ucznia z kilku klas itd. itp.
Twierdzenie:
Jeżeli zdarzenia B1, B2, B3, ...., Bn ⊂Ω i spełniają one warunki:
1) każde dwa zdarzenia parami są rozłączne, tzn. Bi∪Bj=ϕ, gdzie i, j = 1, 2, ..., n i i≠j;
2) B1∪ B2∪ B3∪ .... ∪ Bn =Ω
3) P(B1)>0 i P(B2>0 i ... i P(Bn)>0
to dla dowolnego zdarzenia A⊂Ω zachodzi związek:
Schemat dla prawdopodobieństwa całkowitego

Zadanie 1
W urnie U1 jest 6 kul białych i 4 kule czarne, a w urnie U2 znajdują się 4 białe i 8 czarnych. Rzucamy kostką do gry. Jeżeli wypadnie liczba oczek podzielna przez trzy, to losujemy dwie kule z urny U1 w przeciwnym razie losujemy dwie kule z urny U2. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Rozwiązanie:
Do czynienia mamy tutaj z prawdopodobieństwem całkowitym, składającym się z dwóch etapów:
Etap I - rzut kostką 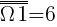 :
:
B1 - zdarzenie, w którym liczba wyrzuconych oczek jest podzielna przez trzy 
B2 - zdarzenie, w którym liczba wyrzuconych oczek jest niepodzielna przez trzy 
Etap II - losowanie kul z odpowiedniej urny
A - zdarzenie, w którym wylosowano dwie kule białe.

![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2995.gif) | [2] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 2
W pewnej grupie ludzi dane dotyczące płci i koloru oczu pokazują poniższe wykresy.

Wybrano losowo jedną osobę, jakie jest prawdopodobieństwo tego, że ma ona zielone oczy?
Rozwiązanie:
Doświadczenie dwuetapowe:
I etap - losowanie osoby ze względu na płeć:
B1 - zdarzenie, w którym wylosowano chłopaka;
B2 - zdarzenie, w którym wylosowano dziewczynę
II etap - sprawdzanie koloru oczu wylosowanej osoby
Dn - dziewczyna z niebieskimi oczami;
Dz - dziewczyna z zielonymi oczami oczami;
Chn - chłopak z niebieskimi oczami;
Chz - chłopak z zielonymi oczami;
[rys} src="rysunki/d_020.png" alt="drzewo prawdopodobieństwa całkowitego zdarzeń do zadania 2" nr="3" description="Drzewo prawdopodobieństwa całkowitego zdarzeń."[/rys]A - zdarzenie, w którym wylosowano osobę z zielonymi oczami
 |
[3] |
Zadanie 3
Uczniowie zorganizowali loterię fantową. Przygotowali 150 wśród których 10 wygrywa. Kupujący los ma do wyboru dwa warianty: I los kupiony z pojemnika, w którym są wszystkie losy; II losy umieszczone są w trzech pojemnikach: zielonym, gdzie znajduje się 47 losów pustych i 5 wygrywających; czerwonym, gdzie znajduje się 45 losów pustych i 5 wygrywających; czarnego, gdzie znajduje się 48 losów pustych i 2 losy wygrywające. Kupujący rzuca kostką, jeżeli wypadnie 6 to losuje z pojemnika czerwonego, jeżeli 5 lub 4 to z zielonego, w pozostałych przypadkach z czarnego. Który z wariantów jest bardziej korzystny dla kupującego?
Rozwiązanie:
Wariant I
Doświadczenie jednoetapowe, 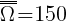
A - zdarzenie, w którym kupiono los wygrywający, 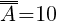
 |
[3] |
Doświadczenie dwuetapowe:
Etap I - rzut kostką 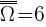 :
:
B1 - zdarzenie, w którym wypadło 6 oczek
B2 - zdarzenie, w którym wypadło 4 lub 5 oczek
B3 - zdarzenie, w którym wypadło 1, 2 lub 3 oczek
Etap II - losowanie losu z odpowiedniego pudła.
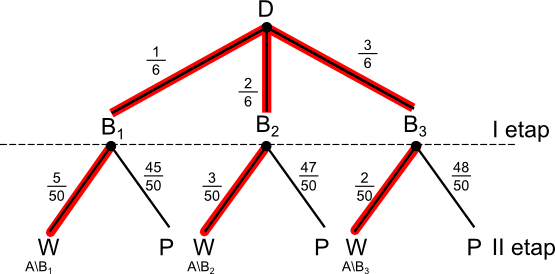
A - zdarzenie, w którym wylosowano los wygrywający.
 |
[4] |
Prawdopodobieństwo wygrania w wariancie pierwszym jest o jeden procent większe niż w wariancie drugim.

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2996.gif)