Stronę tą wyświetlono już: 2805 razy

Równania liniowe z jedną niewiadomą, których najprostsza postać jest następująca:

[1]

Zapis wyrażenia w formacie TeX-a:

a\cdot x+b=0

Zadanie 1

Uprościć i rozwiązać równanie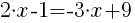

Rozwiązanie:

W pierwszej kolejności wszystkie czynniki, przy których stoi niewiadoma (w tym przypadku x) przenieść należy na prawą stronę równania, a czynniki wolne (baz zmiennej x) na lewą, pamiętając o zmianie znaku na przeciwny podczas przenoszenia. W rozpatrywanym przypadku wygląda to następująco:

[2]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}2\cdot x+3\cdot x=9+1 \\ 5\cdot x=10\end{matrix}

Powyższą uproszczoną postać równania dzielimy obustronnie przez współczynnik stojący przy niewiadomej x aby wyznaczyć w ten sposób jego wartość:

[3]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}5\cdot x=10 {/}:5 \\ x=2\end{matrix}

Zadanie 2

Bochenek chleba kosztuje tyle co 1 zł i pół bochenka chleba. Ile kosztuje chleb?

Rozwiązanie:

Niech c oznacza cenę bochenka chleba, która (jak wynika z samej treści zadania) jest równa , a więc równanie będzie wyglądało następująco:

[4]

Zapis wyrażenia w formacie TeX-a:

c=1+\frac{1}{2}\cdot c

Należy oczywiście przekształcić powyższe równanie, wyznaczając niewiadomą c w następujący sposób:

[5]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}c-\cfrac{1}{2}\cdot c=1 \\ \cfrac{1}{2}\cdot c=1 {/}\cdot 2 \\ c=2\end{matrix}

A więc bochenek chleba kosztuje 2 złote

Zadanie 3

Mietek postanowił wybrać się na pieszą wycieczkę, pierwszego dnia przebył 40 km zaś drugiego połowę tego co pierwszego, trzeciego dnia przebył z kolei 1/4 tego co dnia pierwszego. Ile Mietek przedrałował kilometrów łącznie?

Rozwiązanie:

Zadanie proste, niechaj d oznacza całą drogę, jaką Mietek pokonał podczas wycieczki, więc logicznym jest ułożenie następującego równania:

[6]

Zapis wyrażenia w formacie TeX-a:

p=40+\frac{40}{2}+\frac{40}{4}=70

Mietek przeszedł w trzy dni 70 km

Zadanie 4

Mietek chodzi na siłownię, podnosząc tam ciężar równy połowie masy jego ciała powiększonej o 20kg. Oblicz masę Mietka, wiedząc że podnosi on 50kg ciężar.

Rozwiązanie:

Przez m oznaczmy masę Mietka, równanie będzie miało więc następującą postać:

[7]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}\cfrac{1}{2}\cdot m+20=50 \\ m=60\end{matrix}

Mietek waży 60kg