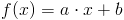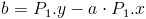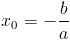Funkcje liniowe

Stronę tą wyświetlono już: 5195 razy

Funkcją liniową nazywa się funkcję następującej postaci:

[1]

Zapis wyrażenia w formacie TeX-a:

f(x)=a\cdot x+b

gdzie:

• a - parametr kierunkowy funkcji f(x), który jest równy tangensowi kąta α zawartego pomiędzy osią x a linią wykresu funkcji f(x) ;
• b - parametr przesunięcia funkcji równy wartości funkcji f(x) dla x=0.

Funkcję linową można opisać za pomocą dwóch nie pokrywających się punktów, w takim przypadku możliwe jest wyznaczenie wzoru na prostą przechodzącą przez owe punkty poprzez wyznaczenie parametrów a i b w następujący sposób:

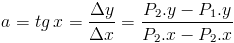[2]

Zapis wyrażenia w formacie TeX-a:

a=tg\,x=\frac{\Delta y}{\Delta x}=\frac{P_2.y-P_1.y}{P_2.x-P_2.x}

założenia:

• P₁≠P₂ - punkty się nie pokrywają;
• Δx≠0 - przyrost odległości pomiędzy punktami na osi x jest różny od zera.

gdzie:

• P₁, P₂ - punkty, przez które przechodzi prosta
• Δx, Δy - przyrost odległości pomiędzy punktami P₁, P₂

[3]

Zapis wyrażenia w formacie TeX-a:

b=P_1.y-a\cdot P_1.x

Miejsce zerowe funkcji liniowej można wyznaczyć przekształcając wzór [1] do następującej postaci:<

[4]

Zapis wyrażenia w formacie TeX-a:

x_0=-\frac{b}{a}

Wyznaczanie punktu przecięcia się dwóch funkcji liniowych f(x) i g(x) jest możliwe tylko wtedy, gdy spełniony jest następujący warunek: a₁≠a₂, przy czym gdy a₁=a₂ oraz b₁=b₂ funkcje f(x), g(x) pokrywają się i mają nieskończenie wiele wspólnych punktów. W przypadku, gdy a₁=a₂ i b₁≠b₂ funkcje f(x), g(x) są równoległe i nie mają punktów wspólnych.

W przypadku, gdy funkcje f(x) i g(x) mają jeden punkt wspólny, możliwe jest jego wyznaczenie poprzez przyrównanie stronami obu tych funkcji w następujący sposób:

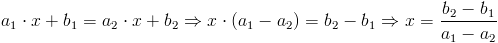[5]

Zapis wyrażenia w formacie TeX-a:

a_1\cdot x+b_1=a_2\cdot x+b_2\Rightarrow x\cdot \left(a_1-a_2\right)=b_2-b_1\Rightarrow x=\frac{b_2-b_1}{a_1-a_2}

Dla x wyznaczonego ze wzoru [5] wartości funkcji f(x), g(x) w tymże punkcie są takie same i stanowią współrzędną y punktu przecięcia się tych funkcji.

Własności funkcji liniowych

Dla wartości parametru a

=0 funkcja liniowa jest funkcją stałą i nie ma miejsc zerowych gdy b≠0, lub ma ich nieskończenie wiele gdy b=0, przeciwdziedzina funkcji przyjmuje wartość stałą równą parametrowi b;

<0 funkcja jest malejąca w całym zbiorze dziedziny funkcji D_f, w przedziale od -∞ do -b/a funkcja jest dodatnia, natomiast w przedziale od -b/a do ∞ funkcja jest ujemna;

>0 funkcja jest rosnąca w całym zbiorze dziedziny funkcji D_f, w przedziale od -∞ do -b/a funkcja jest ujemna, natomiast w przedziale od -b/a do ∞ funkcja jest dodatnia.