Funkcje zależności położenia w różnych układach odniesienia
Stronę tą wyświetlono już: 3981 razy
Istnieją takie przypadki ruchu, które wymuszają określone położenie obiektu np. w kierunku osi y w zależności od położenia obiektu w kierunku osi x. Mowa jest więc tutaj o funkcji y=f(x), która będzie w określony sposób uzależniała położenie obiektu na osi y od położenia na osi x.
Te same zależności można spokojnie wykorzystać również w układach trójwymiarowych tworząc funkcje y=f(x) oraz z=g(x) jak również w układach współrzędnych biegunowych, walcowych a nawet jak ktoś będzie miał taką potrzebę w układach sferycznych.
Zadanie 1
Sanie pociągowe suportu poprzecznego tokarki zostały sprzężone z liniałem sinusoidalnym, którego kąt względem osi x znajdującej się w osi obrotu wrzeciona tokarki wynosi 5°. Wychylenie noża tokarskiego w pozycji początkowej x0=0 jest równe 20[mm]. Znajdź funkcję odchylenia końcówki narzędzia w zależności jego położenia na osi x względem punktu x0.
Dla lepszego zrozumienia, tokarka jest to obrabiarka umożliwiająca wykonywanie przedmiotów o określonych kształtach obrotowych. Na poglądowym rysunku 1 widać sposób w jaki tokarka za pomocą liniału sinusoidalnego może toczyć powierzchnie stożkowe.
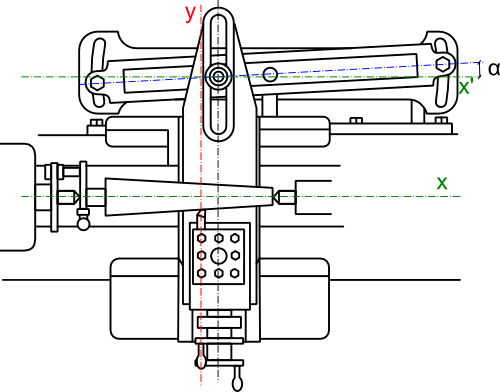
Wydaje się być oczywistym, że mamy tutaj do czynienia z funkcją liniową postaci y=a·x+b, parametr a jest równy:
Z kolei współczynnik b można w łatwy sposób obliczyć wiedząc, że dla x0=0 funkcja f(x)=20[mm], a więc b jest dane następującą zależnością:
Ostatecznie więc szukana przez nas funkcja ma następującą postać:
Zadanie 2:
Skok śruby pociągowej uniwersalnej tokarki TUG-48 wynosi p=12[mm], wyznaczyć funkcję położenia suportu poprzecznego tokarki w zależności od ilości obrotów wykonanych śrubą pociągową licząc od pozycji x0=0 i φ0 = 0°.
Skok gwintu śruby pociągowej p jest to odległość o jaką suport wzdłużny tokarki przesunie się, gdy śruba pociągowa wykona jeden pełny obrót (czyli obróci się o 360°).
Z powyższego wynika, że szukana funkcja x(φ) będzie przyjmowała następującą postać:
Wzór [4] jest wzorem operującym nie na układzie współrzędnych kartezjańskich, ale na układzie współrzędnych walcowych, gdzie x jest zależny od kąta φ.
Zadanie 3
Wyznaczyć funkcję położenia punktów A i B okręgu toczącego się bez poślizgu po płaskiej płaszczyźnie w układzie kartezjańskim z rysunku 2 w zależności od promienia R tegoż okręgu i kąta jego obrotu φ, którego początkowa wartość φ0=0.
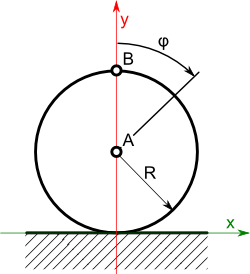
Trzeba odkopać z czeluści zapomnienia stary dobry wzór na długość łuku w zależności od jego kąta, albowiem tak dziwnie się składa, że w tenże jakże przebiegły sposób można obliczyć przemieszczenie środka okręgu (a więc punktu A) względem osi x. Tak więc wzór ten wygląda następująco:
W wzorze [5] kąt φ jest wyrażony w radianach. Jak już wspomniałem wcześniej funkcje określające współrzędne punktu A w zależności od promienia R oraz obrotu o kąt φ przyjmują więc następującą postać:
Przemieszczenie punktu B będzie złożeniem funkcji przemieszczenia środka okręgu (którym jest oczywiście punkt A) oraz przemieszczenia punktu B względem punktu A. Funkcje opisujące przemieszczenie punktu A są już znane, bo przecież chodzi tutaj o wzory [6] i [8] pozostało jedynie wyprowadzić wzór na przemieszczenie punktu B względem punktu A przy pomocy funkcji trygonometrycznych:
Ostatecznie więc:
Jeżeli Twoją głowę zaprząta pytanie, jak będzie wyglądał wykres takiej funkcji w zależności od kąta obrotu okręgu φ, to czym prędzej przestań się zamartwiać, albowiem poniżej jest wykres pokazujący trajektorię przemieszczenia punktu B.
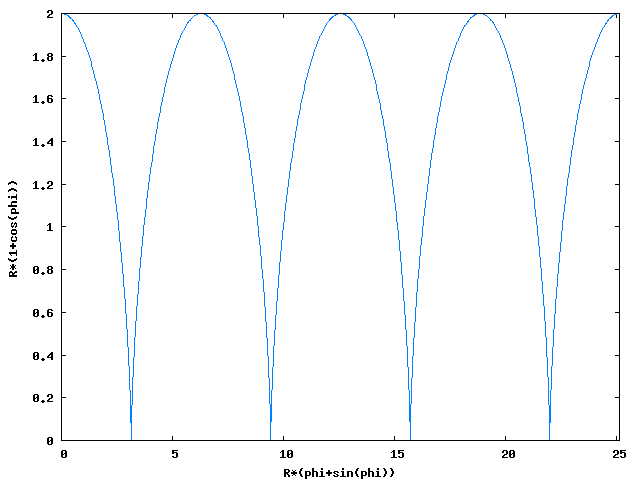
Wykres wygenerowany w programie wxMaxima za pomocą następującego polecenia:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2362.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2363.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2364.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2365.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2366.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2367.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2368.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2369.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2370.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2371.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2372.gif)
