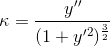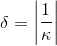Krzywizna i promień funkcji

Stronę tą wyświetlono już: 1154 razy

Obliczanie krzywizny κ i promienia δ funkcji jest przydatne przy wyznaczaniu przyspieszenia stycznego a_st i normalnego a_n punktu poruszającego się po zadanej funkcji trajektorii ruchu.

Krzywizną funkcji nazywamy elementarny stosunek przyrostu kąta d φ do elementarnej długości łuku funkcji zawartej między tymi stycznymi dS. Zapisać można to następująco:

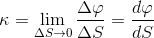[1]

Zapis wyrażenia w formacie TeX-a:

\kappa=\lim_{\Delta S \rightarrow 0}{\frac{\Delta \varphi}{\Delta S}}=\frac{d \varphi}{d S}

Wzór na krzywiznę funkcji danej zależnością y=f(x) w danym punkcie P przyjmuje następującą postać:

[2]

Zapis wyrażenia w formacie TeX-a:

\kappa=\frac{y ''}{(1+y '^2)^\frac{3}{2}}

Wzór na krzywiznę funkcji parametrycznych y=P_y(t), x=P_x(t) w danym punkcie P przyjmuje następującą postać:

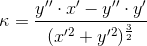[3]

Zapis wyrażenia w formacie TeX-a:

\kappa=\frac{y ''\cdot x '-y ''\cdot y '}{(x '^2+y '^2)^\frac{3}{2}}

Wzór na krzywiznę funkcji r=φ(t) dla danego puntu P w układzie współrzędnych biegunowych:

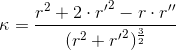[4]

Zapis wyrażenia w formacie TeX-a:

\kappa=\frac{r^2+2\cdot {r'}^2-r\cdot r ''}{(r^2+{r '} ^2)^\frac{3}{2}}

Skoro znany jest już wzór na krzywiznę kappa funkcji, to teraz pora na wzór na promień δ funkcji:

[5]

Zapis wyrażenia w formacie TeX-a:

\delta=\left|\frac{1}{\kappa}\right|

Komentarze