Równanie drogi w zlażności od czasu s(t)
Stronę tą wyświetlono już: 8757 razy
Wiemy już, jak tworzyć równania ruchu r(t), prędkości V(t) i przyspieszenia a(t) chwilowego. Znane są nam również metody obliczania przyspieszenia stycznego ast i normalnego an, to czego nie wiemy to jak obliczyć drogę danego punktu po torze jego ruchu r(t).
Ułóżmy takie oto równanie różniczkowe:
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2596.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
Przekształcając równanie [1] otrzymuje się ogólny wzór na drogę punktu po czasie s(t):
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2597.gif) | [2] |
Zapis wyrażenia w formacie TeX-a:
Ktoś może powiedzieć, cóż w tym takiego trudnego, wystarczy scałkować i ma się wzór na drogę po czasie s(t) i tutaj niestety się mylicie, ponieważ taka całka oblicza drogę uwzględniając kierunek przemieszczenia, przez co dla funkcji okresowych obliczona całka musi zostać podzielona na przedziały, w których wzór na całkowitą drogę będzie inny od otrzymanej wartości całkowej. Wynika to z faktu, że droga s nie uwzględnia w żaden sposób kierunku elementarnego przemieszczenia (zlicza wszystkie wartości bezwzględne przemieszczeń elementarnych).
Zadanie 1
Bazując na treści i rozwiązaniu zadania 2 z strony Fizyka → Kinematyka → Funkcje zależności przemieszczenia, prędkości i przyspieszenia w różnych układach odniesienia wyznaczyć wzór na drogę s(t) rozpatrywanego punktu B z rysunku 1.
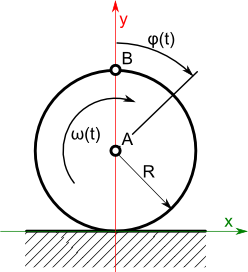
Pochodne równania ruchu po czasie r(t) zostały już policzone w zadaniu 2 i są one dane następującym równaniem ruch V(t):
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2598.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
Wartość wektora całkowitej prędkości chwilowej jest więc równa:
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2599.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
Lewa strona równania [4] to nic innego jak droga po czasie  , a więc po przekształceniu pozostaje do policzenia następująca całka:
, a więc po przekształceniu pozostaje do policzenia następująca całka:
![Równanie [5]](https://obliczeniowo.com.pl/rownania/2600.gif) | [5] |
Zapis wyrażenia w formacie TeX-a:
Po scałkowaniu otrzymuje się następujący wzór, który jest prawdziwy dla s(t≤1):
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2601.gif) | [6] |
Zapis wyrażenia w formacie TeX-a:
Dla t mieszczącego się w przedziale 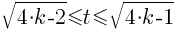 , gdzie
, gdzie  wzór na drogę s(t) przyjmuje postać następującą:
wzór na drogę s(t) przyjmuje postać następującą:
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2602.gif) | [7] |
Zapis wyrażenia w formacie TeX-a:
Dla t mieszczącego się w przedziale 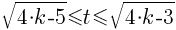 , gdzie
, gdzie  wzór na drogę s(t) przyjmuje postać następującą:
wzór na drogę s(t) przyjmuje postać następującą:
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2603.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Wykres funkcji s(t) dla R=1 i  można zobaczyć na poniższym rysunku.
można zobaczyć na poniższym rysunku.
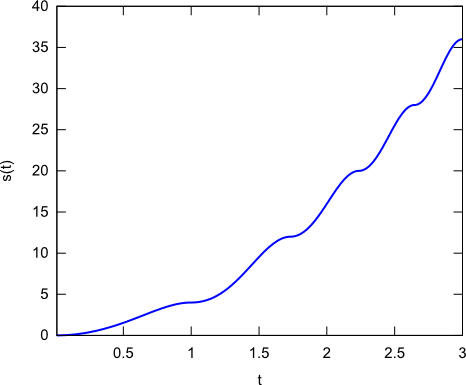

Wykres wygenerowany do pliku svg w programie wxMaxima, za pomocą następującego kodu:
Z wykresu pokazanego na rysunku 2 wynika, że dla 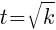 , gdzie
, gdzie 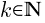 droga s(t) może zostać obliczona ze wzoru:
droga s(t) może zostać obliczona ze wzoru:
Cóż to oznacza zapytacie? Otóż oznacza to tylko tyle, że gdy okrąg z rysunku 1 obróci się o kąt φ=π to punkt B pokona drogę po łuku danym wcześniej już liczonymi funkcjami parametrycznymi jego położenia od czasu równą 4·R. Czyli na każde pół obrotu okręgu, punkt B przemierza drogę równą 4·R.
Zadanie 2
Wyznaczyć równanie drogi w zależności od czasu s(t) dla okręgu jak na rysunku 3 obracającego się wokół osi z prędkością kątową ω=2·π, którego promień R jest znany.

Najpierw wyznaczyć należy równanie zależności kąta od czasu φ(t) licząc całkę z prędkości kątowej:
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2605.gif) | [10] |
Zapis wyrażenia w formacie TeX-a:
Równania parametryczne położenia w zależności od czasu:
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2606.gif) | [11] |
Zapis wyrażenia w formacie TeX-a:
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_2607.gif) | [12] |
Zapis wyrażenia w formacie TeX-a:
Pochodne parametrycznych funkcji położenia po czasie:
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2609.gif) | [14] |
Zapis wyrażenia w formacie TeX-a:
Równanie drogi w zależności od czasu s(t):
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2610.gif) | [15] |
Zapis wyrażenia w formacie TeX-a:

![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2604.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2608.gif)
