Minory macierzy

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 45130 razy

Dla dowolnej macierzy o wymiarach n×m, gdzie dla n i m nie mogą być jednocześnie równe 1 można wyznaczyć minory, które stanowią wyznaczniki takiej macierzy, która powstała z danej macierzy A w wyniku skreślenia co najmniej jednej kolumny lub jednego wiersza.

Przykład

Weźmy sobie macierz następującej postaci:

M=delim{[}{matrix{4}{5}{ {4} {2} {3} {5} {6} {7} {8} {9} {10} {2} {3} {1} {3} {7} {9} {4} {1} {2} {5} {7} } }{]}

Wykreślając kolumnę 4-tą uzyskuję minor:

$A_M=delim{|}{ matrix{4}{4}{ {4} {2} {3} {6} {7} {8} {9} {2} {3} {1} {3} {9} {4} {1} {2} {7}} }{|}$

Istnieje pewna szczególna grupa minorów macierzy zwanych minorami głównymi, dla których przy wykreślaniu pozostawiono wiersze i kolumny o takich samych indeksach. W wcześniej rozpatrywanym przykładzie nie mamy do czynienia z minorem głównym ponieważ w wyniku wykreślenia kolumny 4-tej pozostały kolumny o indeksach: 1; 2; 3 i 5 oraz wiersze o indeksach: 1; 2; 3 i 4.

Wykreślmy więc z macierzy M kolumny 4-tą i 5-tą oraz wiersz 4-ty otrzymując minor następującej postaci:

$B_M=delim{|}{ matrix{3}{3}{ {4} {2} {3} {7} {8} {9} {3} {1} {3} } }{|}$

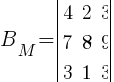
W powyższym przypadku pozostawiono kolumny: 1; 2 i 3 oraz wiersze 1; 2 oraz 3 a więc mamy tutaj do czynienia z minorem głównym macierzy M .

Na tym jednak nie koniec, albowiem istnieją takie minory główne, które mają ten zaszczyt nazywać się wiodącymi minorami głównymi. Taki wiodący minor główny powstaje wtedy, gdy skreślamy ostatnie wiersze i/lub kolumny macierzy.

Dla przykładu weźmy sobie naszą nieszczęsną macierz M, skreślmy jej ostatnią kolumnę, otrzymując jej wiodący minor główny następującej postaci:

$C_M=delim{|}{matrix{4}{4}{ {4} {2} {3} {5} {7} {8} {9} {10} {3} {1} {3} {7} {4} {1} {2} {5} } }{|}$

Idąc dalej, wykreślmy sobie dwie ostatnie kolumny i jeden wiersz naszej macierzy M otrzymując tym samym kolejny wiodący wyznacznik główny macierzy M:

$D_M=delim{|}{matrix{3}{3}{ {4} {2} {3} {7} {8} {9} {3} {1} {3} } }{|}$

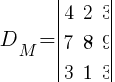
Posuwając się o kolejny krok do przodu i skreślając trzy ostatnie kolumny i dwa ostatnie wiersze macierzy M otrzymujemy następny wiodący minor główny macierzy M:

$E_M=delim{|}{matrix{2}{2}{ {4} {2} {8} {3} } }{|}$

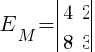
Istnieje już tylko jeden wiodący minor główny macierzy M, którego jeszcze nie wyznaczyliśmy, a powstanie on ze skreślenia czterech ostatnich kolumn i trzech ostatnich wierszy macierzy M:

$F_M=delim{|}{4}{|}$

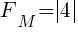
Z minorami macierzy mamy do czynienia przy obliczaniu wyznacznika z macierzy kwadratowej metodą Laplace'a, jak również przy obliczaniu macierzy odwrotnej A^-1.

Strony powiązane

Minor macierzy