Stronę tą wyświetlono już: 22550 razy

Z przyczyn czysto technicznych w rysunku dla krawędzi powierzchni okrągłych stosuje się konstrukcję zastępczą elipsy, którą jest owal. Metodę kreślenia owali omówiłem już wcześniej na stronie Geometria wykreślna → Podstawowe konstrukcje → Kreślenie owali. Ponieważ izometryczne rysunki stanowią dość szczególny przypadek, który upraszcza do minimum kreślenie owali, z tego też względu na wcześniej wspomnianej stronie interesował nas będzie jedynie rysunek 4.

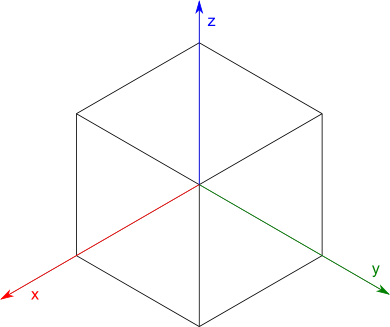
Wykonajmy sobie takie oto ćwiczenie: w izometrii wykonać rysunek sześcianu o dowolnej długości boku a (zalecam długość 50mm na kartce A4, a następnie w każdą z trzech widocznych płaszczyzn sześcianu wpisać owal stosując konstrukcję zastępczą elipsy.

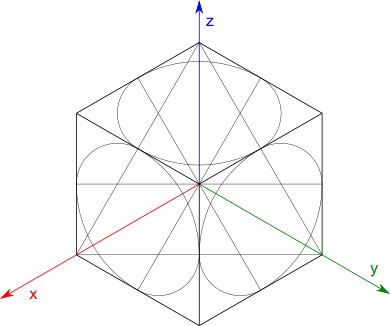
Po wpisaniu w ściany sześcianu owali, powinno się otrzymać rysunek jak poniżej.

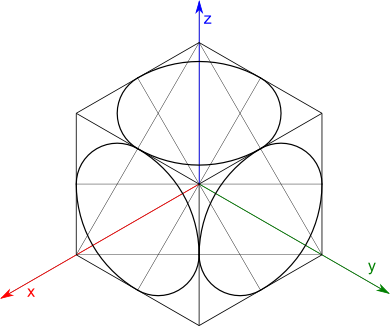
W końcowym etapie pogrubić krawędzie owali.

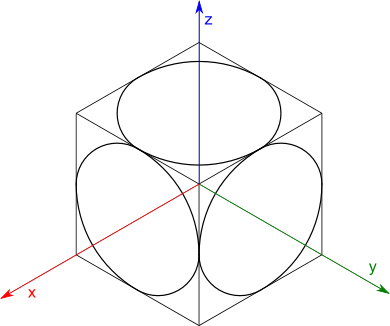
I na końcu pozbyć się linii pomocniczych kreślenia konstrukcji owali.

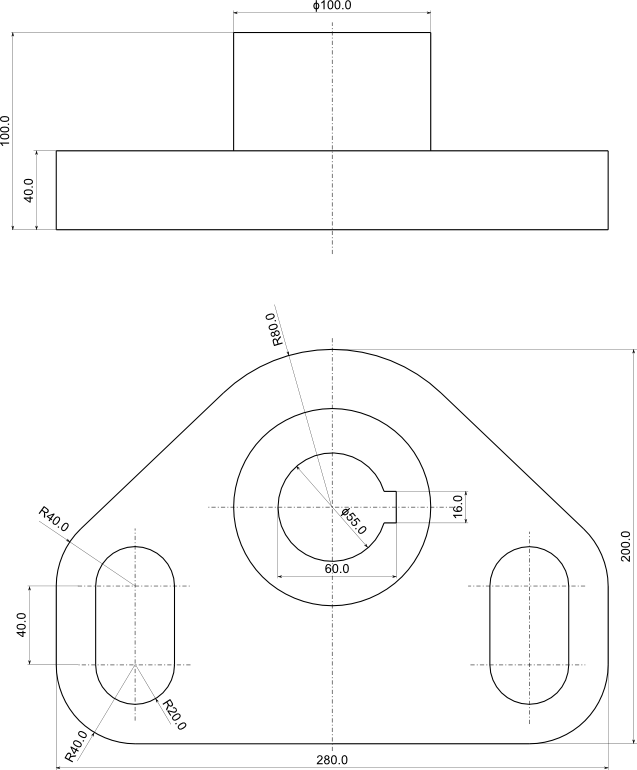
Kolejne ćwiczenie: na podstawie rysunku 5 wykreślić w izometrii obiekt nań opisany w skali: dla formatu A4 - 1:2 lub dla formatu A3 - 1:1.

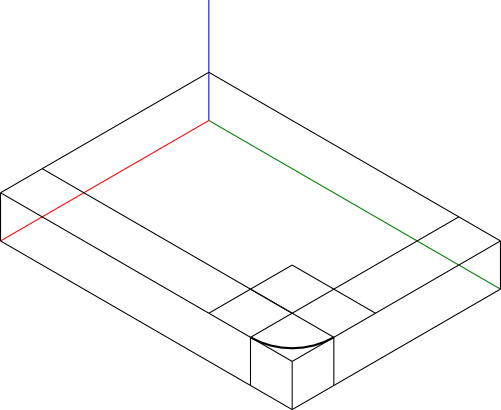
Jak widać na rysunku 5 obiekt został pokazany w dwóch rzutach, jego płaską podstawę można wpisać w prostopadłościan o wymiarach 280×200 (jednostką jest oczywiście mm). Z tego też względu czym prędzej narysujmy taką oto roboczą konstrukcję pomocniczą pokazaną na rysunku 6.

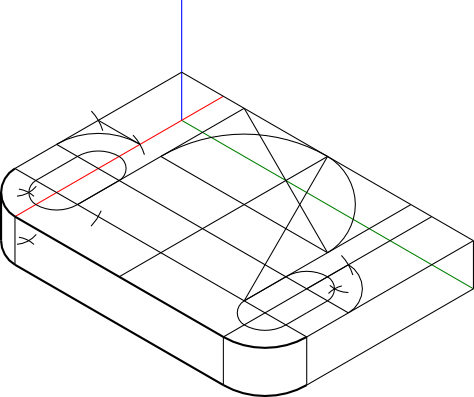
Teraz można zacząć to, co tygrysy lubią najbardziej, czyli wykreślić pomocniczą konstrukcję, która ma na celu naniesienie pierwszego łuku krawędzi podstawy obiektu. W tym celu konieczne jest wyznaczenie linii odległych o 40 mm od dolnego narożnika prostopadłościanu oraz rombu o długości boku 80 mm, dzięki czemu można wykreślić pierwszy łuk krawędzi podstawy.

Ponieważ nie ma co stać jak cieć przy hałdzie żwiru i czekać na cud, więc zabierzmy się teraz za wyznaczenie łuku dla kolejnych krawędzi jak na rysunku 8.

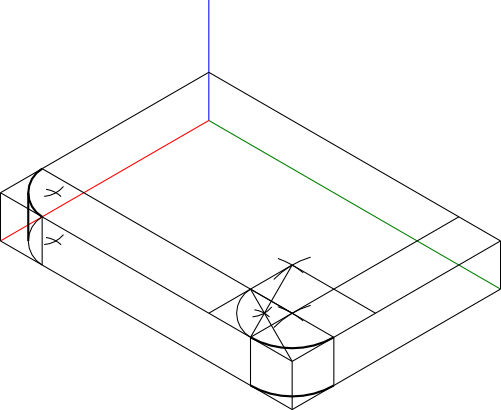
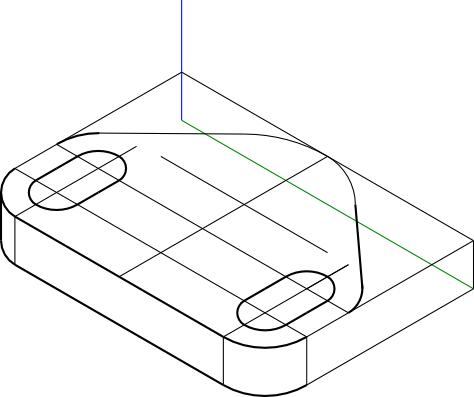
Zabierzmy się w końcu za otwory zakończone półokręgami tworząc dla nich również pomocniczą konstrukcję jak poniżej.

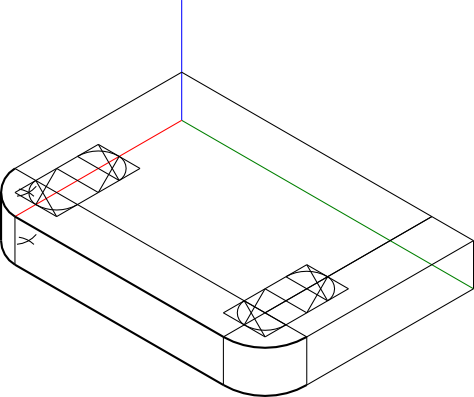
Nadeszła stosowna chwila ku temu, by zabrać się za wyznaczenie łuków o promieniu 40 mm i 80 mm

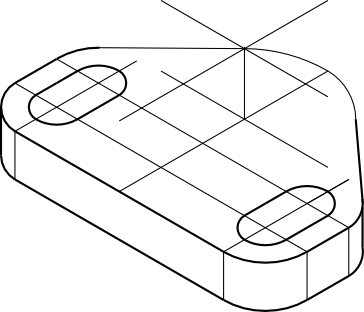
Uporządkujmy nieco rysunek 10 wymazując co jest nam już niepotrzebna i pogrubiając już niektóre linie.

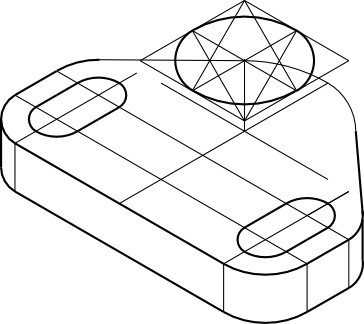
Wyznaczamy wysokość i osie symetrii walcowej części obiektu jak poniżej.

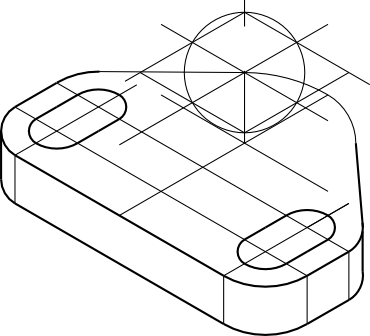
Teraz w znany już sposób trzeba wykreślić konstrukcję, niezbędną do wykreślenia elipsy zewnętrznej powierzchni walcowej.

Skoro mamy już siatkę to wykreślenie owalu będzie dziecinnie proste.

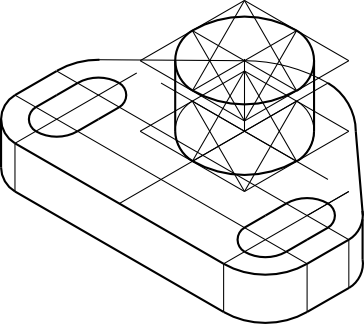
Zabieramy się za powierzchnię walcową w podstawie obiektu.

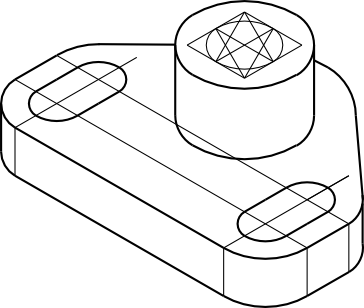
Uporządkujmy nieco rysunek i dodajmy do niego owal wewnętrznej krawędzi otworu.

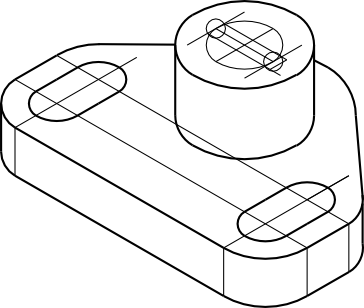
Teraz trzeba znaleźć krawędzie wpustu, którego odległość jest mierzona od przeciwległej krawędzi otworu.

Ostatecznie więc rysunek końcowy będzie wyglądał tak jak poniżej.

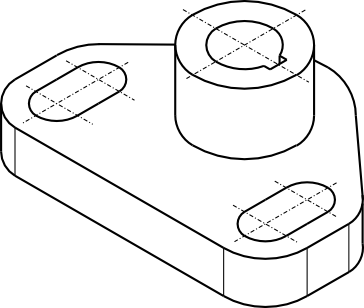
Pokusiłem się również o stworzenie wersji modelu 3W w programie OpenSCAD, którą można zobaczyć na poniższym rysunku.