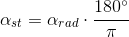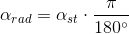Stronę tą wyświetlono już: 26926 razy

Definicja kąta płaskiego

Kątem płaskim nazywa się zbiór płaszczyzn jednej z dwóch części zawartych na i pomiędzy dwiema półprostymi k i m charakteryzującymi się wspólnym początkiem. Półproste k, m nazywane są ramionami kąta.

W przestrzeni 2W powyższa definicja kąta zamienia się z płaszczyzn do półprostych zawartych pomiędzy jedną z dwóch części wraz z półprostymi k i m.

Miara kąta płaskiego

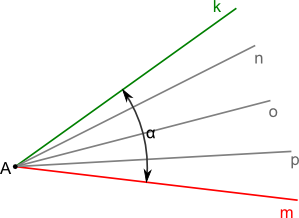
Na rysunku 1 oznaczenie α jest miarą kata. Umownie do oznaczania kątów używa się małych liter alfabetu greckiego. Spis nazw i symboli poszczególnych liter można zobaczyć na stronie Dodatki tabelaryczne → Alfabet grecki.

Miarą kąta są stopnie kątowe ° oraz radiany. W stopniach kątowych kąt pełny wynosi 360°, natomiast w radianach 2·π. Przelicznikiem z radianów na stopnie jest więc następujący wzór:

[1]

Zapis wyrażenia w formacie TeX-a:

\alpha_{st}=\alpha_{rad}\cdot\frac{180^{\circ}}{\pi}

Wzór odwrotny, przeliczający z stopni na radiany otrzymuje się po przekształceniu wzoru [1] do postaci następującej:

[2]

Zapis wyrażenia w formacie TeX-a:

\alpha_{rad}=\alpha_{st}\cdot\frac{\pi}{180^{\circ}}

Klasyfikacja kątów płaskich

Stosuje się podział kątów płaskich ze względu na ich miarę:

1) kąty ostre - to kąty o mierze mniejszej niż 90° lub 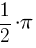[rad];

2) kąty proste - to kąty o mierze równej 90° lub 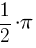[rad];

3) kąty rozwarte - to kąty o mierze większej od 90° lub 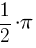[rad] oraz mniejszej lub równej 180° lub π [rad];

4) kąty wypukłe - to kąty o mierze mniejszej lub równej 180° lub π [rad] oraz równej 360° lub 2·π [rad];

5) kąty wklęsłe - to kąty o mierze większej od 180° lub π [rad] a zarazem mniejszej od 360° [rad] lub 2·π [rad]

Wyznaczanie siecznej kąta za pomocą linijki i cyrkla

Sieczna kąta jest to taka półprosta, która dany kąt α dzieli na dwa przystające (takie same) kąty.

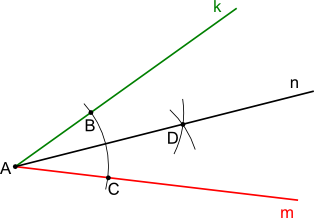
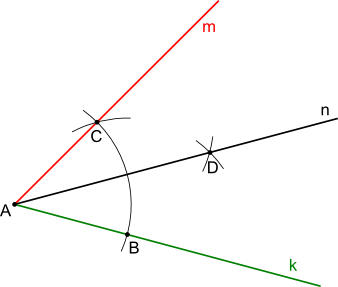
Na rysunku 2 widoczna jest konstrukcja siecznej kąta płaskiego, gdzie półprosta n została wyznaczona poprzez wyznaczenie punktów przecięcia się łuku o dowolnym promieniu r zakreślonego z punktu A z półprostymi m oraz k. Z w ten sposób uzyskanych punktów B i C tą samą rozwartością cyrkla zakreślić łuki, których punkt przecięcia D wyznacza przejście półprostej n będącej sieczną danego kąta.

Wyznaczania znanych wartości kątów za pomocą cyrkla i linijki

Wyznaczanie kąta 60°

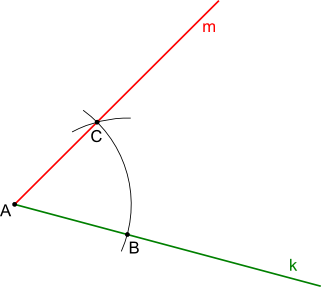
Należy wykreślić dowolną półprostą k o początku w punkcie A, z którego to dowolną rozwartością cyrkla należy wyznaczyć punkt B. Następnie tą samą rozwartością cyrkla z punktu A oraz B zakreślić łuki, których przecięcie wyznaczy punkt C. Przez punkty C i A należy poprowadzić półprostą m. Kąt zawarty pomiędzy półprostymi k i m jest równy 60°.

Wyznaczanie kąta 30°

Kąt 30° można uzyskać poprzez wyznaczenie siecznej kąta 60°, a konstrukcje kąta 60° jak i siecznej są już znane.

Wyznaczanie kąta 120°

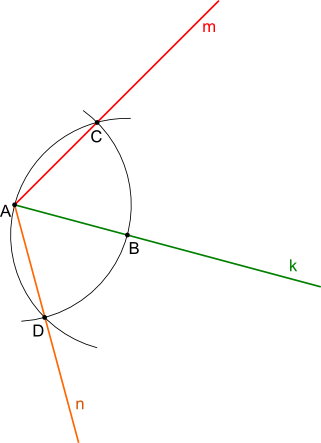
Konstrukcja kąta 120° jest bardzo podobna do konstrukcji kąta 60°. Narysujmy półprostą k o punkcie początkowym A, z którego to zakreślić należy dowolną rozwartością cyrkla łuk wyznaczający punkt B na półprostej k. Z punktów A i B tą samą rozwartością cyrkla co poprzednio zakreślić łuki, których punkty przecięcia wyznaczą półproste m i n. Kąt zawarty pomiędzy półprostymi m i n jest równy 120°.

Wyznaczanie kąta prostego

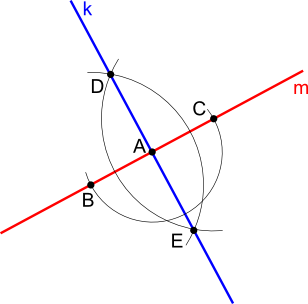
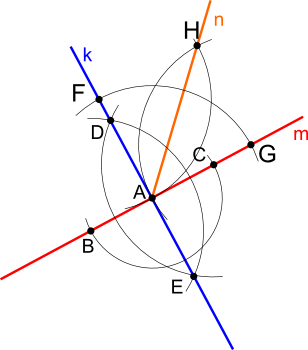
Na dowolnej prostej m należy obrać punkt A, z którego to dowolną rozwartością cyrkla należy wyznaczyć punkty B i C. Z tychże punktów dowolną rozwartością cyrkla należy zakreślić łuki, których punkty przecięcia D i E wyznaczają prostą k. Wszystkie kąty zawarte pomiędzy prostymi k i m są kątami prostymi.

Wyznaczanie kąta 45°

Kąt 45° można wyznaczyć wykorzystując konstrukcję kąta prostego i siecznej tak jak widać to na rysunku 7.