Wielokąty płaskie

Stronę tą wyświetlono już: 20040 razy

Wielokąty płaskie - definicja

Istnieje pewna grupa szczególnych rodzajów figur płaskich, zwana wielokątami. Aby dana figura płaska mogła być zaliczona do wielokątów płaskich muszą zostać spełniać następujące warunki:

1. boki figury składają się z prostokreślnych odcinków, które tworzą zamkniętą przestrzeń 2W;
2. wierzchołki takiej figury muszą leżeć na jednej płaszczyźnie płaskiej, stanowiącej przestrzeń 2W.

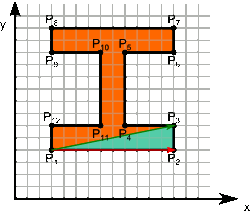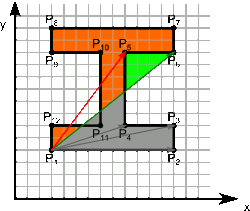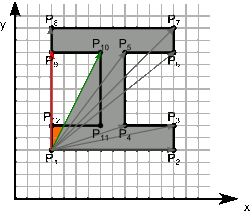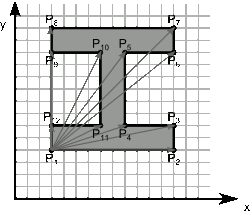
Każdy wielokąt opisuje się za pomocą zbioru punktów, które stanowią wierzchołki danej figury płaskiej. Dla przykładu dany jest wielokąt płaski ABCDEF jak na rysunku 1, jak widać kolejność poszczególnych punktów determinuje kolejność łączenia wierzchołków.

Podział wielokątów płaskich

Wielokąty wypukłe

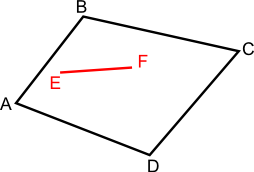
Wielokąty wypukłe to takie, dla których każdy odcinek, którego końce leżą wewnątrz wielokąta zawiera się całkowicie w takim wielokącie.

Definicję wielokąta wypukłego można określić również następująco: dany wielokąt jest wypukły, jeżeli wartość mniejszego kąta zawartego pomiędzy każdą parą boków wychodzących z danego wierzchołka wielokąta zawiera się wewnątrz tego wielokąta.

Matematycznie rzecz ujmując, można skorzystać z wzoru [7] z strony Matematyka → Wektory → Wyznacznik dwóch wektorów aby stwierdzić, że dla wszystkich trzech sąsiadujących wierzchołków danego wielokąta płaskiego wartość takiego wyznacznika ma taki sam znak.

Wszystkie trójkąty należą do zboru wielokątów wypukłych.

Wielokąty wklęsłe

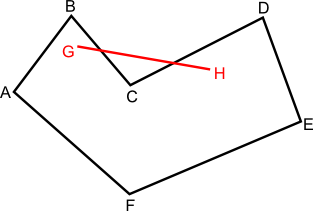
Każdy wielokąt, dla którego da się określić taki odcinek, którego końce znajdują się w jego wnętrzu i sam ten odcinek nie zawiera się całkowicie wewnątrz takiego wielokąta.

Każdy wielokąt, którego dowolny wewnętrzny kąt jest większy od 180° jest wielokątem wklęsłym.

Żaden trójkąt nie należy do zbioru wielokątów wklęsłych.

Wielokąty proste

Wielokąty proste to takie, których boki nie przecinają się oraz nie zawierają w swoim wnętrzu otworów. Każdy trójkąt należy do zbioru wielokątów prostych.

Wielokąty złożone

Wielokąty złożone - to takie, których boki się przecinają lub zawierają w swoim wnętrzu otwór (tak, jak pokazane zostało to na rysunku 6.

Każdy wielokąt złożony składa się z wielokątów prostych.

Wielokąty foremne

Zbiór wielokątów foremnych jest tak wielki, jak zbiór liczb naturalnych z pominięciem zera. Wielokąty foremne mają następujące cechy wspólne:

1. Długości ich boków są sobie równe;
2. Da się w nie oraz na nich opisać okrąg;
3. Kąty zawarte pomiędzy sąsiadującymi bokami są zawsze takie same i wynoszą:

[1]

Zapis wyrażenia w formacie TeX-a:

\alpha=180^\circ-\frac{360^\circ}{n}

gdzie n - oznacza liczbę wierzchołków lub boków wielokąta foremnego.

Wyróżnione typy wielokątów

Wśród zbioru wielokątów są takie, które są wyróżnione nazwami własnymi. Zacznijmy więc od nazewnictwa trójkątów, które dzielą się na:

• równoboczne;
• równoramienne;
• ostrokątne (wszystkie kąty wewnętrzne mniejsze od 90°);
• prostokątne (jeden kąt wewnętrzny jest równy 90° a pozostałe mniejsze);
• rozwartokątne (jeden kąt wewnętrzny jest większy od 90° a pozostałe mniejsze)

W świecie czworokątów wyróżnia się:

• kwadraty - będące szczególną postacią rombu;
• prostokąty - będące szczególną postacią równoległoboku;
• romby;
• równoległoboki;
• trapezy:
  • równoramienne;
  • różnoramienne;
  • prostokątne;
• deltoidy

Obwód wielokąta prostego

Dla każdego wielokąta prostego jego obwodem jest suma długości jego boków. Z tego też względu, znając współrzędne poszczególnych wierzchołków danego wielokąta prostego można jego obwód obliczyć za pomocą następującego wzoru, wykorzystującego rachunek wektorowy:

[2]

Zapis wyrażenia w formacie TeX-a:

L=\left|\vec{P}_1-\vec{P}_n\right|+\sum_{i=1}^{n-1}{\left|\vec{P}_i-\vec{P}_{i+1}\right|}

gdzie n jest oczywiście liczbą wierzchołków lub boków wielokąta prostego.

Pole powierzchni wielokąta prostego

Pole powierzchni można obliczyć korzystając z wzoru [1] lub [2] z strony Matematyka → Wektory → Obliczanie pól powierzchni figur płaskich. Poniżej przytaczam owe wzory:

[3]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=\frac{1}{2}\cdot\left|\sum_{i=2}^{i=n-1}\left(\vec{P}_i-\vec{P}_1\right)\times\left(\vec{P}_{i+1}-\vec{P}_1\right)\right|

Powyższa wersja wykorzystuje iloczyn wektorowy dwóch wektorów, natomiast poniżej znajduje się wersja z wyznacznikiem dwóch wektorów:

[4]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=\frac{1}{2}\cdot\left|\sum_{i=2}^{i=n-1}Det\left(\vec{P}_i-\vec{P}_1,\,\vec{P}_{i+1}-\vec{P}_1\right)\right|=\frac{1}{2}\cdot\left|\sum_{i=2}^{i=n-1}\begin{vmatrix} \vec{P}_{i\rightarrow x} - \vec{P}_{1\rightarrow x} & \vec{P}_{i+1\rightarrow x} - \vec{P}_{1\rightarrow x} \\ \vec{P}_{i\rightarrow y} - \vec{P}_{1\rightarrow y} & \vec{P}_{i\rightarrow y} - \vec{P}_{1\rightarrow y} \end{vmatrix}\right|

Poniżej z kolei zamieszczam animację pokazującą, jak obliczane jest za pomocą wzorów [3] i [4] pole powierzchni wielokąta prostego.