Czworokąty - podstawowe typy i wzory
Stronę tą wyświetlono już: 74090 razy
Podstawowe typy czworokątów
W świecie czworokątów znajdują się takie, które ze względu na swój kształt i częstość występowania w obliczeniach zostały wyróżnione nazwami własnymi. Do tego typu czworokątów należą:
- kwadraty
- prostokąty
- romby
- równoległoboki
- trapezy
- różnoramienne
- równoramienne
- prostokątne
- deltoidy
- wypukłe
- wklęsłe
Wszystkie kształty czworokątów można zobaczyć na rysunku 1 poniżej.
Suma kątów wewnętrznych każdego czworokąta jest zawsze równa 360° lub 2·π.
Czworokąty mogę być w odróżnieniu od trójkątów wklęsłe lub wypukłe, istnieje również możliwość utworzenia czworokąta złożonego (samoprzecinającego się).
Podstawowe wzory
Kwadraty
Kwadrat należy do rodziny wielokątów foremnych i jako taki spełnia następujące cechy wielokątów foremnych:
- wszystkie długości jego boków są takie same;
- na jego wierzchołkach da się opisać okrąg;
- w jego wnętrze da się wpisać okrąg;
- wszystkie kąty wewnętrzne kwadratu mają taką samą wartość i wynoszą 90°
Obwód kwadratu (jak możecie się domyślić) jest więc równy:
Pole powierzchni kwadratu jest równie łatwo obliczyć z następującego wzoru:
Ponieważ kwadrat ma również dwie przekątne d, których długość jest równa:
dlatego też można napisać wzór na pole powierzchni kwadratu związany z przekątną, przyjmujący postać następującą:
Promień okręgu opisanego na kwadracie jest równy:
Natomiast promień okręgu wpisanego w kwadrat wynosi:
Większość tych wzorów wynika z samej ilustracji kwadratu, którą poniżej zamieszczam.
Opis oznaczeń:
- A, B, C, D - wierzchołki kwadratu;
- a - boki kwadratu;
- d - przekątne kwadratu;
- Sc - środek ciężkości kwadratu, punkt przecięcia się przekątnych p i środek okręgów: wpisanego i opisanego na kwadracie;
- Rw - promień okręgu wpisanego w kwadrat;
- Ro - promień okręgu opisanego na kwadracie"
- A, B, C, D - wierzchołki prostokąta;
- a - krótsze boki prostokąta;
- b - dłuższe boki prostokąta;
- d - przekątne prostokąta;
- Sc - środek ciężkości prostokąta, punkt przecięcia się jego przekątnych d oraz środek okręgu opisanego na nim;
- Ro - promień okręgu opisanego na prostokącie
- Pk - długość przekątnej krótszej;
- Pk - długość przekątnej dłuższej.
- A, B, C, D - wierzchołki rombu;
- a - boki rombu;
- α - mniejsza wartość wewnętrznego kąta;
- β - większa wartość wewnętrznego kąta;
- h - wysokość rombu;
- Pk - długość krótszej przekątnej rombu;
- Pd - długość dłuższej przekątnej rombu;
- Sc - środek ciężkości rombu, punkt przecięcia się jego przekątnych oraz środek okręgu weń wpisanego;
- r - promień okręgu wpisanego.
- A, B, C, D - wierzchołki równoległoboku;
- a - długość krótszego boku;
- b - długość dłuższego boku;
- α - mniejsza wartość wewnętrznego kąta;
- β - większa wartość wewnętrznego kąta;
- h - wysokość równoległoboku;
- Pk - długość krótszej przekątnej równoległoboku;
- Pd - długość dłuższej przekątnej równoległoboku;
- Sc - środek ciężkości równoległoboku i punkt przecięcia się jego przekątnych;
- γ kąt zawarty pomiędzy przekątnymi równoległoboku.
- a - długość dłuższej podstawy trapezu;
- b - długość krótszej podstawy trapezu;
- c, d - długości ramion trapezu
- a - długość dłuższej podstawy trapezu;
- b - długość krótszej podstawy trapezu;
- c, d - długości ramion trapezu
- A, B, C, D - wierzchołki trapezu;
- a - dłuższa podstawa;
- b - krótsza podstawa;
- c, d - ramiona;
- α, β - kąty wewnętrzne przy dłuższej podstawie a;
- γ, δ - kąty wewnętrzne przy krótszej podstawie b;
- h - wysokość trapezu;
- A, B, C, D - wierzchołki trapezu;
- a - dłuższa podstawa trapezu równoramiennego;
- b - krótsza podstawa trapezu równoramiennego;
- c - ramiona trapezu równoramiennego;
- α - kąty wewnętrzne przy dłuższej podstawie a trapezu równoramiennego;
- β - kąty wewnętrzne przy krótszej podstawie b trapezu równoramiennego;
- h - wysokość trapezu równoramiennego;
- m, n, k - sieczne boków trapezu równoramiennego;
- So - punkt przecięcia się siecznych boków trapezu równoramiennego a zarazem środek okręgu na nim opisanego;
- Ro - promień okręgu opisanego na trapezie równoramiennym;
- p - przekątne trapezu równoramiennego;
- φ - kąt zawarty pomiędzy przekątnymi trapezu;
- F - punkt przecięcia się przekątnych
- A, B, C, D - wierzchołki trapezu;
- a - długość dłuższej podstawy trapezu;
- b - długość krótszej podstawy trapezu;
- c - długość ramienia biegnącego pod kątem ostrym w stosunku do dłuższej podstawy;
- d - długość ramienia trapezu, przy którym kąty wewnętrzne mają wartość równą 90°;
- h - wysokość, która jest równa długości ramienia d trapezu prostokątnego
- a - dłuższa podstawa trapezu;
- b - krótsza podstawa trapezu;
- c, d - dłuższe ramiona trapezu;
- α, β - kąty wewnętrzne trapezu, znajdujące się przy dłuższej jego podstawie;
- Sw - środek okręgu wpisanego;
- Rw - promień okręgu wpisanego;
- k, o - półproste prostopadłe do ramion trapezu;
- m, n - proste, na których leżą ramiona trapezu;
- q, s - proste, na których leżą podstawy trapezu;
- p - prosta równoległa do podstaw trapezu i przechodząca przez środek okręgu wpisanego Sw
- A, B, C i D - wierzchołki deltoidu;
- α β; γ - kąty wewnętrzne deltoidy;
- a - krótsza długość boku deltoidu;
- b - dłuższa długość boku deltoidu;
- pAB - przekątna łącząca wierzchołki A i B, w których zbiegają się boki deltoidu o tych samych długościach;
- pCD - przekątna łącząca wierzchołki C i D, w których zbiegają się boki deltoidu o różnych długościach;
- E - punkt przecięcia się przekątnych w deltoidzie wklęsłym;
- Sw - środek okręgu wpisanego w deltoid wklęsły;
- F - punkt styczności okręgu wpisanego z bokiem a deltoidu;
- Rw - promień okręgu wpisanego w deltoid;
- SDγ - sieczna kąta γ wychodząca z wierzchołka D;
- SCγ - sieczna kąta γ wychodząca z wierzchołka C
Miejsce przecięcia się przekątnych kwadratów Sc nazywa się środkiem jego ciężkości, który leży w połowie jego szerokości i wysokości, które są równe długości jego boku a.
Prostokąty
Prostokąt to figura płaska, której kąty wewnętrzne (tak jak w przypadku kwadratu) są równe 90°, a pary przeciwległych boków mają taką samą długość a i b. Szczególnym przypadkiem prostokąta jest więc kwadrat, gdy długości par boków spełniają warunek a=b.
Obwód prostokąta (jak to zawsze bywa) jest sumą długości jego boków, co można zapisać za pomocą następującego wzoru:
Pole powierzchni prostokąta z kolei opisuje następujący niezwykle trudny do zapamiętania wzór:
Każdy prostokąt ma dwie przekątne d, których długości są sobie równe i wynoszą:
Na prostokącie (co z resztą widać na rysunku 2 widać) można opisać okrąg, którego promień Ro jest równy:
Środek ciężkości prostokąta tak jak w przypadku kwadratu wyznacza punkt przecięcia się dwóch jego przekątnych lub innymi słowy, środek ciężkości prostokąta leży w połowie jego szerokości i połowie jego wysokości.
Opis oznaczeń:
Romby
Romb to czworokąt, którego wszystkie boki mają taką samą długość tak jak ma to miejsce w przypadku kwadratu, natomiast w odróżnieniu od kwadratu jego kąty wewnętrzne dzielą się na dwie pary α i β; których suma jest zawsze równa:
W przypadku, gdy α=β romb jest kwadratem.
Obwód rombu (jak można się domyślić) jest równy:
Natomiast aby obliczyć pole powierzchni rombu trzeba znać długość jego boku a oraz wysokość h:
Pole powierzchni rombu, gdy dana jest wartość mniejszego kąta α i długość boku a:
Gdy dany jest kąt β wystarczy skorzystać ze wzoru:
Przekątne rombu mają różne długości i przecinają się pod kątem prostym. Znając ich długości można obliczyć pole powierzchni rombu z następującego wzoru:
gdzie:
Na rombie nie da się opisać okręgu, gdy α≠β, ale zawsze można weń wpisać okrąg, którego promień jest równy:
Środek ciężkości Sc rombu wyznacza punkt przecięcia się jego przekątnych, który leży w połowie jego wysokości i w połowie jego szerokości wynoszącej a+a·cos α.
Opis oznaczeń:
Równoległobok
Równoległobok to czworokąt, którego przeciwległe pary boków mają taką samą długość (jak w prostokącie) i spełniają one warunek równoległości. Pary owych boków mają różne długości a i b. Kąty wewnętrzne równoległoboku dzielą się na dwie pary α i β, które (tak samo jak w rombie) spełniają równość [11]. Gdy kąty α i beta; są sobie równe, to równoległobok jest prostokątem. Gdy długości boków a i b są równe to równoległobok jest rombem, natomiast gdy dodatkowo jeszcze kąty α i beta; są sobie równe, wtedy równoległobok jest kwadratem.
Obwód równoległoboku można obliczyć z następującego wzoru:
Pole powierzchni równoległoboku można wyliczyć znając długości jego boku a oraz wysokość h na ten bok spuszczonej:
Pole powierzchni równoległoboku można również wyliczyć znając długości jego boków a i b oraz wartość mniejszego kąta α za pomocą takiego oto wzoru:
Znając długość mniejszego kąta zawartego pomiędzy przekątnymi Pk i Pd, których długości również są znane można obliczyć pole powierzchni takiego równoległoboku:
Znając współrzędne kolejnych sąsiadujących z sobą wierzchołków równoległoboku można obliczyć jego pole powierzchni w następujący sposób (dla wierzchołków A, B i C):
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_2043.gif) | [22] |
Zapis wyrażenia w formacie TeX-a:
Zrozumienie powyższego wzoru wymaga znajomości podstaw rachunku wektorowego, który opisany został w dużej mierze przeze mnie w dziale Matematyka → Wektory.
Środek ciężkości Sc równoległoboku wyznacza punkt przecięcia się jego przekątnych i leży on w połowie jego wysokości h i połowie jego całkowitej szerokości, która jest równa a+b·cos α.
Opis oznaczeń:
Trapezy
Trapez to czworokąt, którego dwa przeciwległe boki (nazywane podstawami) są równoległe, a suma kątów leżących przy danym jego ramieniu jest zawsze równa 180°.
Dla trapezu, który ma różne długości ramion obwód wynosi:
gdzie:
Pole powierzchni dla tego samego typu trapezu można obliczyć znając długości podstaw a i b oraz (opcjonalnie) kąt α i długość leżącego przy nim ramienia c lub kąt β oraz długość leżącego przy nim ramienia d:
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_2045.gif) | [24] |
Zapis wyrażenia w formacie TeX-a:
Znając długości podstaw a i b trapezu i jego wysokość można obliczyć jego pole powierzchni z wzoru następującej postaci:
Znając długości poszczególnych boków trapezu, można wyliczyć jego pole powierzchni z następującego wzoru:
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_2047.gif) | [26] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
Powyższy wzór jest spełniony dla a>b a dla b=0 upraszcza się on do postaci wzoru Heroda i trójkąta.
Opis oznaczeń:
Pole powierzchni trapezu równoramiennego, dla którego dana jest długość przekątnych p oraz kąt φ zawarty pomiędzy nimi oblicza wzór:
Powyższy wzór sprawdza się tylko w przypadku trapezów równoramiennych, ponieważ dla wszystkich innych trapezów długości ich przekątnych nie są sobie równe. Trapez równoramienny jest jedynym typem trapezu, na którym można opisać okrąg.
Opis użytych oznaczeń:
Jak widać na rysunku 7 wszystkie symetralne boków trapezu równoramiennego przecinają się w jednym punkcie So, stanowiącym środek okręgu opisanego na tymże trapezie. Wyznaczenie promienia Ro nie jest jednak proste, gdyż wymaga rozwiązania trzech układów równania okręgu dla dowolnych trzech wierzchołków rozpatrywanego trapezu, dzięki czemu można by było obliczyć położenie środka okręgu So oraz jego promienia Ro. Wzór ten wyprowadziłem swego czasu i użyłem w moim programie, który dostępny jest na stronie Programowanie → Algorytmy obliczeniowe → Obliczenie środka okręgu przechodzącego przez trzy punkty. Na tej samej stronie znajdują się wyprowadzone wzory na środek okręgu (w rozpatrywanym tutaj przypadku So), którego znajomość daje podstawę do obliczenia promienia Ro.
Istnieje jeszcze trzeci wyróżniony typ trapezu, który ma co najmniej dwa kąty proste znajdujące się przy tym samym ramieniu. W takim przypadku wysokość h takiego trapezu jest równa długości ramienia d leżącego przy kącie prostym (co widać na rysunku 8). Trapez można traktować jako pewne uogólnienie takich figur płaskich jak: kwadrat, prostokąt, romby czy równoległobok, ponieważ wszystkie te figury spełniają warunek równoległości co najmniej jednej pary boków przeciwległych.
Opis oznaczeń:
Czas porozmawiać o szczególnym rodzaju trapezu, który można wyróżnić we wszystkich wcześniej wymienionych jego typach. Mowa jest tutaj o trapezach, w których wnętrze da się wpisać okrąg. Długości boków trapezów tego typu w ogólnej postaci (czyli dla dowolnych danych kątów α i β ramion c i d oraz promienia Rw) dają się opisać zależnością od owych kątów i promienia. Zależności te postaram się wyprowadzić w miarę jak najbardziej jasny sposób korzystając z rysunku 9.
Opis niektórych oznaczeń:
Konstrukcję z rysunku 9 można wykreślić za pomocą linijki i cyrkla zaczynając od narysowania prostej p, obrania na niej dowolnego punktu Sw, z którego to należy wykreślić okrąg o promieniu Rw. Okrąg ten będzie oczywiście okręgiem wpisanym w trapez. Teraz należy korzystając z konstrukcji kreślenia prostych równoległych (opisanej na stronie Geometria wykreślna → Podstawowe konstrukcje → Kreślenie prostych równoległych) wyznaczyć proste q i s.
Z punktu Sw należy poprowadzić dwie półproste k i o pod dowolnym kątem ostrym względem prostej p. Należy zaznaczyć punkty przecięcia się półprostych k i s z okręgiem wpisanym literami H i F, a następnie poprowadzić proste prostopadłe do półprostych k i o w tychże punktach.
Owe proste m i n wyznaczają następujące punkty przecięcia: prosta m: punkty A; E i F; prosta n punkty: D; F i C, gdzie dla osoby kreślącej taki trapez istotne są punkty A; B; C i D stanowiące wierzchołki trapezu.
W celu wyprowadzenia wzorów, które umożliwią wyliczenie długości boków a, b, c i d na rysunku 9 poprowadzone zostały dwie proste t i w, które są prostopadłe do prostej p i przechodzą: prosta t przez punkt E; prosta w przez punkt F. Nietrudno teraz jest zauważyć, że prosta t tworzy dwa trójkąty przystające: AEP i BES. O tym jak można stwierdzić, że dane dwa trójkąty są przystające pisałem na stronie Matematyka → Geometria → Podobieństwo trójkątów i trójkąty przystające. To samo dotyczy prostej w, która z kolei tworzy dwa następujące trójkąty przystające: DFQ i CFR. Wszystkie te trójkąty są trójkątami prostokątnymi, dla których znany jest jeszcze jeden kąt α w przypadku trójkątów związanych z prostą t i β dla trójkątów związanych z prostą w.
Ponieważ odcinek PS ma długość równą 2·Rw a odcinek EP stanowi połowę odcinka PS przeto ramię c jest równe dwukrotności długości odcinka AE (wynika z praw proporcji). Z tego też płynie wniosek niezbity, że długość ramienia c można obliczyć z następującego wzoru:
Analogicznie w przypadku ramienia d:
Aby wyliczyć długości podstaw a i b trapezu, trzeba najpierw wyznaczyć długość odcinków ESw oraz SwF, które składają się na długość odcinka EF. Długość odcinka ESw należy wyliczyć z trójkąta prostokątnego SwEH, w którym to kąt zawarty pomiędzy ramieniem ESw jest równy α, co umożliwia obliczenie szukanej długości odcinka ESw:
Z trójkąta SwFL można wyliczyć długość boku SwF wiedząc, że kąt zawarty pomiędzy ramionami SwF i FL jest równy β. Ostatecznie więc szukany wzór przyjmuje postać następującą:
Długość odcinka EF jest więc równa:
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_2053.gif) | [32] |
Zapis wyrażenia w formacie TeX-a:
Zanim przejdę do dalszego wyznaczania wzoru na długość podstaw a i b trapezu, warto nadmienić, że długość odcinka EF jest równa połowie sumy ramion trapezu a ta występuje przecież w ogólnym wzorze [25] na pole powierzchni trapezu. Z tego wniosek nasuwa się sam, że pole powierzchni trapezu, w który da się wpisać okrąg o promieniu Rw i którego kąty α i β są dane można obliczyć z następującego wzoru:
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_2054.gif) | [33] |
Zapis wyrażenia w formacie TeX-a:
W powyższym wzorze h zostało zastąpione przez 2·Rw, co wynika z rysunku 9.
Dłuższa podstawa a trapezu dzieli się na trzy odcinki: AP, PQ i QD, z czego odcinek PQ jest równy odcinkowi EF, którego długość jest dana zależnością [32]. Pozostaje więc wyznaczenie długości odcinka AP z trójkąta prostokątnego APE stosując wzór trygonometryczny na tangens kąta α:
Podobnie z trójkąta DFQ można wyliczyć długość odcinka QD:
Ostatecznie więc długość dłuższej podstawy a trapezu, w który da się wpisać okrąg o promieniu Rw i którego kąty α i β są znane wynosi:
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_2057.gif) | [36] |
Zapis wyrażenia w formacie TeX-a:
W podobny sposób można wyznaczyć długość krótszej podstawy b trapezu. W tym jednak przypadku należy zauważyć, że długość odcinka SR pomniejszona o długości odcinków SB i CR jest równa długości c. Tak się szczęśliwie składa, że długość odcinka SB jest równa długości odcinka EF, natomiast długość odcinka SB jest równa długości odcinka AP ponieważ trójkąty APE i BSE są przystające. Również długość odcinka CR jest znana, ponieważ trójkąty CRF i DFQ są przystające, a więc odcinek CR ma długość równą długości odcinka QD. Teraz można napisać następującą zależność długości krótszej podstawy c trapezu od promienia Rw okręgu wpisanego w ten trapez oraz kątów α i β.
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_2058.gif) | [37] |
Zapis wyrażenia w formacie TeX-a:
Deltoidy
Deltoidy - to czworokąty, które składają się z dwóch par boków a i b, gdzie (w odróżnieniu od prostokątów) boki o takich samych długościach mają wspólny wierzchołek. Każdy deltoid ma dwie przekątne: pAB - leżącą przy wierzchołkach A i B, w których łączą się boki deltoidu o takich samych długościach; pCD - łączącej wierzchołki C i D, w których łączą się boki deltoidu o różnych długościach. Przekątne deltoidów zawsze przecinają się (lub ich przedłużenia przecinają się) pod kątem prostym.
Deltoidy mogą być wklęsłe lub wypukłe. Gdy kąt wewnętrzny α zawarty pomiędzy krótszymi bokami a deltoidu jest większy od 180° to taki deltoid jest wklęsły, w przeciwnym przypadku deltoid jest wypukły.
W każdy wypukły deltoid można wpisać okrąg o promieniu Rw. Istnieje tylko jeden szczególny rodzaj deltoidu, na którym można opisać okrąg jest to deltoid o bokach a=b i wszystkich kątach wewnętrznych równych 90°. Nie trudno się domyślić, że taki deltoid jest kwadratem.
Szczególnymi postaciami deltoidu są: kwadrat i romb.
Obwód deltoidu to suma długości jego boków:
Długość boków deltoidu można obliczyć znając kąty α i β oraz długość przekątnej PCD za pomocą następujących wzorów:
Podstawiając zależności [39] i [40] do wzoru [38] można uzyskać nową postać wzoru na obwód deltoidu, który z najdzikszą wręcz rozkoszą zamieszczam poniżej:
![Równanie [41]](https://obliczeniowo.com.pl/rownania/w_2062.gif) | [41] |
Zapis wyrażenia w formacie TeX-a:
Znając długości boków a i b oraz wartości kątów α i β można obliczyć pole powierzchni deltoidu z następującego wzoru:
![Równanie [42]](https://obliczeniowo.com.pl/rownania/w_2063.gif) | [42] |
Zapis wyrażenia w formacie TeX-a:
Powyższy wzór można zastąpić następującą wersją:
gdzie kąt γ można wyznaczyć z następującej zależności:
Ostatni wzór, na pole powierzchni, gdy dane są długości przekątnych pAB i pCD deltoidu ma postać następującą:
Promień okręgu wpisanego Rw można wyznaczyć znając długość przekątnej pCD i kątów α oraz γ z następującej zależności:
![Równanie [46]](https://obliczeniowo.com.pl/rownania/w_2067.gif) | [46] |
Zapis wyrażenia w formacie TeX-a:
I to by było na tyle, jeżeli chodzi o wzory związane z deltoidami, poniżej jeszcze zamieszczam ilustrację przykładowych deltoidów.
Opis oznaczeń:
Czworokąty - ostateczne starcie
Na koniec pragnę zamieścić dwa wzory, wykorzystujące rachunek wektorowy, a które umożliwiają obliczenie obwodu i pola powierzchni każdego czworokąta prostego. Dane, jakie trzeba posiadać to współrzędnej wierzchołków A, B, C i D.
Tak więc obwód można obliczyć z następującego wzoru:
![Równanie [47]](https://obliczeniowo.com.pl/rownania/w_2068.gif) | [47] |
Zapis wyrażenia w formacie TeX-a:
Pole powierzchni natomiast można obliczyć z wzoru:
![Równanie [48]](https://obliczeniowo.com.pl/rownania/w_2069.gif) | [48] |
Zapis wyrażenia w formacie TeX-a:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2024.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2025.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2026.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2027.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2028.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2029.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2030.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2031.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2032.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2033.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2034.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2035.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2036.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2037.gif)
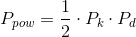
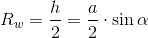
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_2040.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_2041.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_2042.gif)
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_2044.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_2046.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_2048.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_2049.gif)
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_2050.gif)
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_2051.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_2052.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_2055.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_2056.gif)
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_2059.gif)
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_2060.gif)
![Równanie [40]](https://obliczeniowo.com.pl/rownania/w_2061.gif)
![Równanie [43]](https://obliczeniowo.com.pl/rownania/w_2064.gif)
![Równanie [44]](https://obliczeniowo.com.pl/rownania/w_2065.gif)
![Równanie [45]](https://obliczeniowo.com.pl/rownania/w_2066.gif)