Podstawowe wzory

Stronę tą wyświetlono już: 1678 razy

Pochodna funkcji stałej:

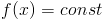
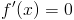
f(x)=const f'(x)=0 [1]

Pochodna funkcji potęgowej:

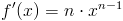
f(x)=x^n f'(x)=ncdot x^{n-1} [2]

gdzie:

  • n - wykładnik funkcji potęgowej

Pochodna funkcji podpierwiastkowej:

f(x)=sqrt[n]{x^m}=x^{frac{m}{n}} f'(x)=frac{m}{n}cdot x^{frac{m}{n}-1}=frac{m}{n}cdot x^{frac{m-n}{n}} [3]

Pochodne funkcji trygonometrycznych:

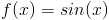
f(x)=sin(x) f'(x)=cos(x) [4]
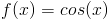
f(x)=cos(x) f'(x)=-sin(x) [5]
f(x)=tan(x) f'(x)=frac{1}{cos^2,x} [6]
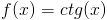
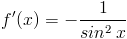
f(x)=ctg(x) f'(x)=-frac{1}{sin^2,x} [7]

Pochodne funkcji wykładniczych:

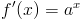
f(x)=a^x f'(x)=a^xcdot ln, a [8]

gdzie:

  • a - parametr funkcji wykładniczej

Gdy a=e funkcja f(x) oraz pochodna przyjmują następującą postać:

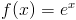
f(x)=e^x f'(x)=e^x [9]

Pochodne funkcji logarytmicznych:

Pochodna logarytmu naturalnego:

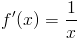
f(x)=ln,x f'(x)=frac{1}{x} [10]

Pochodna logarytmu o podstawie a:

f(x)=log _ax f'(x)=frac{1}{xcdot ln,a} [11]

Pochodne funkcji cyklometrycznych:

f(x)=arc,sin,x f'(x)=frac{1}{sqrt{1-x^2}} [12]
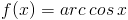
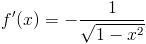
f(x)=arc,cos,x f'(x)=-frac{1}{sqrt{1-x^2}} [13]
f(x)=arc,tan,x f'(x)=frac{1}{1+x^2} [14]
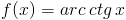
f(x)=arc,ctg,x f'(x)=-frac{1}{1+x^2} [15]

Komentarze