Podstawowe twierdzenia o pochodnych funkcji
Stronę tą wyświetlono już: 6747 razy
Pochodna iloczynu stałej c i funkcji f(x) jest równa iloczynowi stałej c i pochodnej funkcji f(x).
Przykład
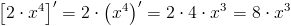 |
Zapis wyrażenia w formacie TeX-a:
Pochodna funkcji f(x) będącej sumą funkcji składowych g(x), h(x) jest równa sumie pochodnych funkcji składowych. To samo twierdzenie stosuje się dla różnicy funkcji składowych, z czego wynika, że pochodna jest rozdzielna względem operatorów dodawania i odejmowania.
Przykład
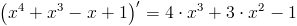 |
Zapis wyrażenia w formacie TeX-a:
Pochodna funkcji f(x) składającej się z iloczynu funkcji g(x), h(x) jest równa sumie iloczynu pochodnej funkcji g(x) i niezmienionej funkcji h(x) oraz iloczynu niezmienionej funkcji g(x) i pochodnej funkcji h(x).
![f'(x)=left[g(x)cdot h(x)right]'=g'(x)cdot h(x)-g(x)cdot h'(x)](https://obliczeniowo.com.pl/rownania/w_1274.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
Przykład
Pochodna iloczynu funkcji składowych g(x), h(x)
 | [5] |
Zapis wyrażenia w formacie TeX-a:
Przykład
 |
Zapis wyrażenia w formacie TeX-a:
Pochodna funkcji złożonej f(x)=g[h(x)] jest równa iloczynowi pochodnej funkcji zewnętrznej g[h(x)] oraz funkcji wewnętrznej h(x).
Przykład
![Przykład obliczania pochodnej funkcji złożonej f(x)=g[h(x)]](https://obliczeniowo.com.pl/rownania/w_1278.gif) |
Zapis wyrażenia w formacie TeX-a:

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota


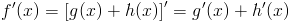


![Wzór na pochodną funkcji złożonej f(x)=g[h(x)]](https://obliczeniowo.com.pl/rownania/w_1279.gif)