Wyznaczanie punktów przebicia kuli z prostą
Stronę tą wyświetlono już: 8493 razy
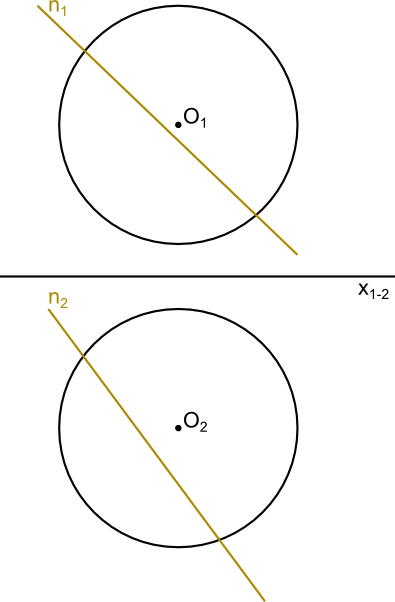
A niechaj istnieje taka kula i niechaj istnieje taka prosta n, taka że w pewnych punktach P1 i P2 przebija ona bezlitośnie daną kulę. Poniżej zamieszczona została ilustracja do tego zadania.
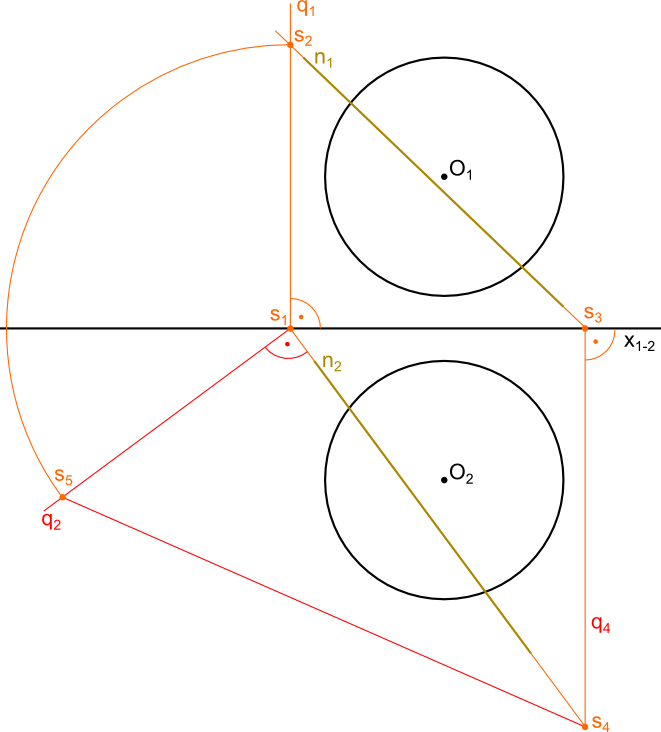
Zadanie należy rozpocząć od przedłużenia rzutów prostej n do momentu przecięcia się ich z linią osi x1-2 a następnie z uzyskanych w ten jakże przebiegły sposób punktów s1 i s2 poprowadzić proste prostopadłe do osi rzutni x1-2 i znaleźć punkty s4 i s5. Teraz z punktu s1 rozwartością cyrkla równą odległości dzielącej tenże punkt od punktu s3 wyznaczyć punkt s5, który należy niezwłocznie połączyć linią z punktem s4.
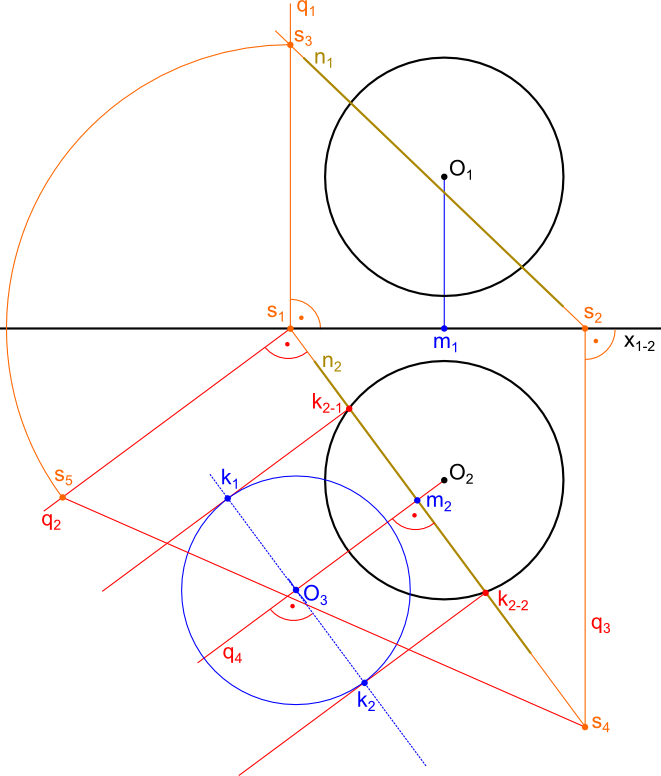
Konieczne jest wyznaczenie prostej prostopadłej do rzutu prostej n2, która jednocześnie przechodzi przez środek kuli O2 wyznaczając tym samym punkt pomocniczy m2. Odległością równą dystansowi dzielącemu punkt O1 od jego rzutu na oś x1-2 (czyli od punktu m1) zakreślić z punktu m2 łuk wyznaczając w ten sposób punkt O3. Zaznaczyć należy sobie punkty k2-1 i k2-2, które wyznacza przecięcie się rzutu prostej n2 z krawędzią rzutu kuli. Z tychże punktów czym prędzej należy poprowadzić proste prostopadłe do rzutu prostej n2. Z kolei przez punkt O3 poprowadzić należy prostą równoległą do rzutu prostej n2 wyznaczając tym samym punkty k1 oraz k2. Rozwartością cyrkla równą odległości punktu O3 od wcześniej wspomnianych punktów zakreślić okrąg.
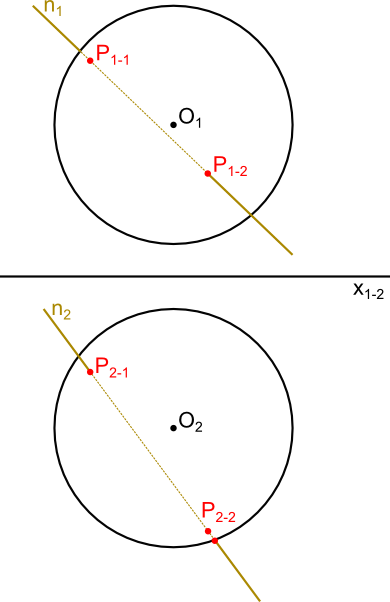
Punkty P1 i P2 przecięcia się narysowanego wcześniej okręgu z odcinkiem łączącym punkty s4 i s5 należy zrzutować prostopadle na rzut prostej n2 wyznaczając tym samym punkty przebicia kuli P2-1 i P2-2 na rzutni π2. Oczywistym wydaje się fakt, że wystarczy teraz zrzutować te punkty na rzutnię π1 by uzyskać punkty P1-1 i style="color:red">P1-2.
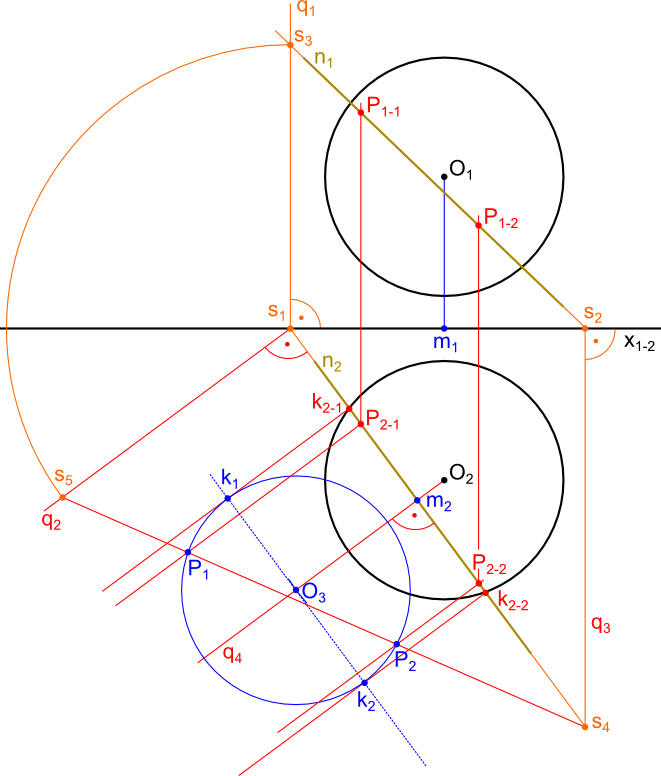
Teraz pozostało już tylko zaznaczenie widoczności, jak uczyniłem to na poniżej ilustracji.
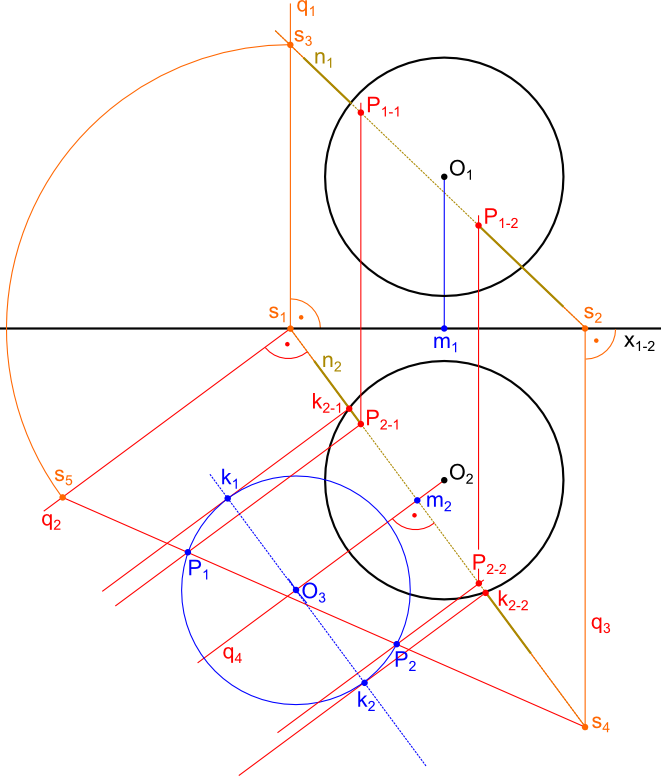
Oczywiście wypadałoby na koniec oczyścić rysunek z zbędnych już linii pomocniczych, co też i z najdzikszą rozkoszą czynię załączając poniższy rysunek.