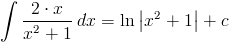Podstawowe właściwości
Autor podstrony: Krzysztof Zajączkowski
Stronę tą wyświetlono już: 2070 razy
Całka iloczynu stałej a i funkcji f(x) jest równa iloczynowi stałej i całki z funkcji f(x).
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1358.gif) |
[1] |
Zapis wyrażenia w formacie TeX-a:
\int c\cdot f(x),dx=c\cdot \int f(x),dx
Przykład
Zapis wyrażenia w formacie TeX-a:
\int \frac{3}{\sqrt{2}}\cdot x^2\,dx=\frac{3}{\sqrt{2}}\cdot\int x^2\, dx=\frac{3}{\sqrt{2}}\cdot \frac{1}{3}\cdot x^3=\frac{x^3}{\sqrt{2}}=\frac{x^3\cdot \sqrt{2}}{2}
Całka z funkcji składającej się z sumy lub różnicy funkcji jest równa sumie lub iloczynowi tych funkcji składowych.
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1360.gif) |
[2] |
Zapis wyrażenia w formacie TeX-a:
\int \left[f(x)\pm g(x)\right]\,dx=\int f(x)\,dx\pm\int g(x)\,dx
Przykład
Zapis wyrażenia w formacie TeX-a:
\int\left(x^2+3\cdot x\right)\,dx=\int x^2\,dx+3\cdot \int x\,dx=\frac{x^3}{3}+\frac{3\cdot x^2}{2}+c=\frac{2\cdot x^3+9\cdot x^2}{6}+c
Całka z ilorazu pochodnej funkcji f'(x) i funkcji f(x) jest równa logarytmowi naturalnemu funkcji f(x)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1362.gif) |
[3] |
Zapis wyrażenia w formacie TeX-a:
\int \frac{f'(x)}{f(x)}, dx=\ln|f(x)|+c
Przykład
Zapis wyrażenia w formacie TeX-a:
\int \frac{2\cdot x}{x^2+1}\,dx=\ln \left|x^2+1\right|+c
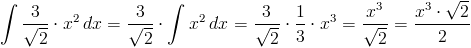
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1360.gif)
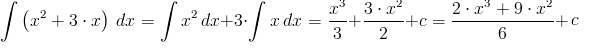

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1358.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1362.gif)