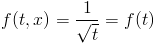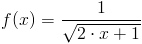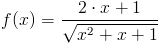Całkowanie przez podstawienie
Stronę tą wyświetlono już: 4785 razy
Całkowanie przez podstawienie funkcji f(x) jest możliwe gdy istnieje taka funkcja g(x) stanowiąca część funkcji f(x), której wartość przypisana do dowolnie obranej zmiennej pomocniczej np. t jest podstawiana do funkcji f(x) otrzymując tym samym funkcję f(t,x). Konieczne jest również wyznaczenie wartości dx względem dt poprzez obliczenie pochodnej dt=g'(x) dx. Iloraz funkcji f(t,x), g'(x) musi być równy funkcji f(t), innymi słowy dzielenie przez pochodną funkcji g'(x) powinno zredukować niewiadomą x w funkcji f(t,x), tak aby w ten sposób otrzymana została funkcja zależna od zmiennej t.
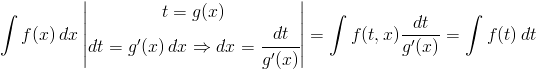 | [1] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- g(x) - wyodrębniona funkcja wewnętrzna funkcji f(x);
- f(t,x) - funkcja powstała z podstawienia do funkcji f(x) za g(x) zmiennej t (gdy w funkcji wyeliminowane zostaną wszystkie wyrażenia zawierające niewiadomą x funkcja ta jest funkcją f(t) a pochodna funkcji g(x) nie może zawierać zmiennej x);
- f(t) - funkcja całkowicie zależna od zmiennej t.
Oczywiście wykonywanie podstawienie ma sens jedynie wtedy, gdy daje ono odpowiednie uproszczenie funkcji f(x) do postaci możliwej do scałkowania. Do funkcji pierwotnej F(x) uzyskanej po scałkowaniu funkcji f(t) podstawić należy za t wartość funkcji g(x) otrzymując tym samym upragnioną funkcję pierwotną F(x).
Zadanie 1 Obliczyć całkę następującej funkcji:
Należy wyodrębnić w funkcji f(x) pod funkcję g(x) sprawiającą kłopoty w scałkowani funkcji f(x), w tym przypadku g(x)=x+1. A więc zmienna pomocnicza będzie równa:
zaś pochodna powyższej równości:
Do wzoru funkcji f(x) podstawić za wyrażenie g(x) zmienną t otrzymując funkcję f(t,x):
Funkcja f(t,x) tak naprawdę w tym przypadku uprościła się do funkcji f(t), ponieważ w jej wyrażeniu nie występuje zmienna x. Stosunek funkcji f(t) do funkcji g'(x) jest równy f(t), tak więc można rozpocząć obliczenia.
![obliczenie całki z funkcji [2]](https://obliczeniowo.com.pl/rownania/w_1369.gif) | [6] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 2 Obliczyć całkę następującej funkcji:
Tym razem nie będę się rozpisywał za bardzo jak w poprzednim przypadku, tym bardziej, że funkcja jest podobna do tej z zadania 1:
![obliczenie całki z funkcji [7]](https://obliczeniowo.com.pl/rownania/w_1371.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 3 Obliczyć całkę następującej funkcji:
Rozwiązanie:
![obliczenie całki z funkcji [9]](https://obliczeniowo.com.pl/rownania/w_1372.gif) | [10] |
Zapis wyrażenia w formacie TeX-a:

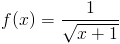
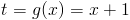
![pochodna równania [3]](https://obliczeniowo.com.pl/rownania/w_1367.gif)