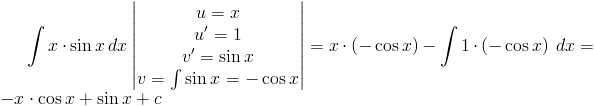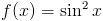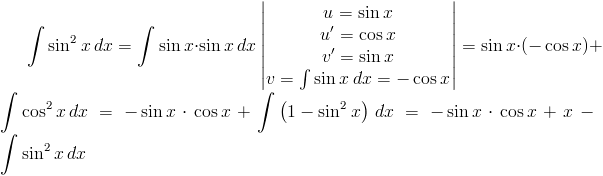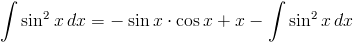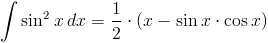Całkowanie przez części

Stronę tą wyświetlono już: 3411 razy

Całkowanie przez części jest kolejną metodą całkowania funkcji. Wzór ogólny tej metody całkowania ma następującą postać:

[1]

Zapis wyrażenia w formacie TeX-a:

\int u(x)\cdot v'(x)\, dx=u(x)\cdot v'(x)-\int u'(x)\cdot v(x)\,dx

Równanie [1] można udowodnić w następujący sposób:

Całkując przez części używa się następującego zapisu:

[2]

Zapis wyrażenia w formacie TeX-a:

\int f(x)\cdot g(x)\,dx\begin{vmatrix} u=f(x)\\ u'=f'(x)\\ v'=g(x)\\ v=\int g(x)\, dx\end{vmatrix}=f(x)\cdot \int g(x)\,dx-\int f'(x)\cdot \left[\int g(x)\,dx\right]\,dx

Zadanie 1 Obliczyć całkę z następującej funkcji:

Rozwiązanie:

Zadanie 2 Obliczyć całkę z następującej funkcji:

Rozwiązanie:

Przyrównując pierwszy człon powyższego równania i przyrównując go do ostatniego otrzymuje się następującą równość:

po odpowiednim przekształceni otrzymuje się upragnioną całkę funkcji sin²x: