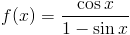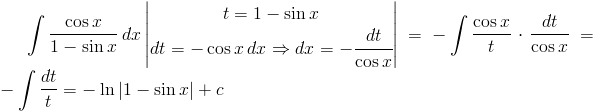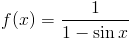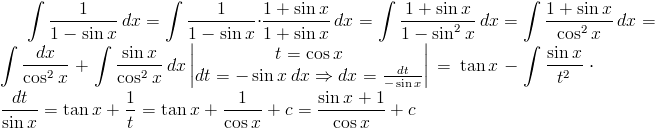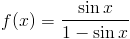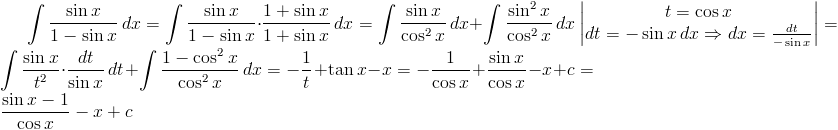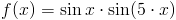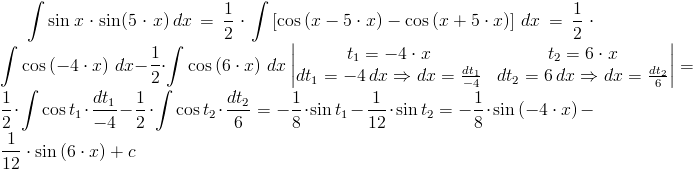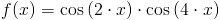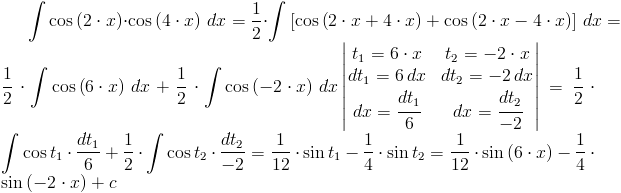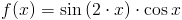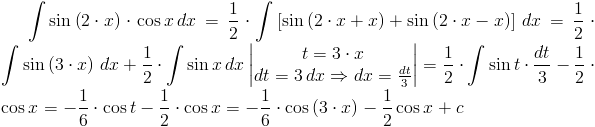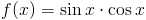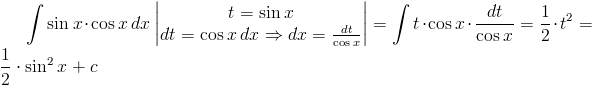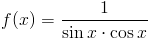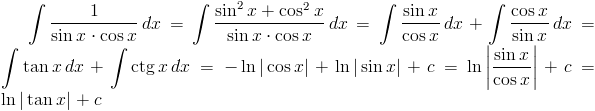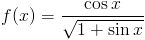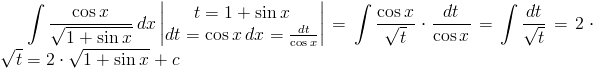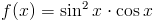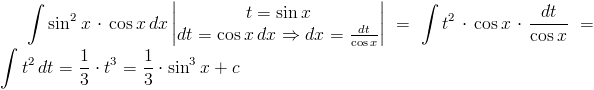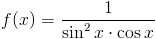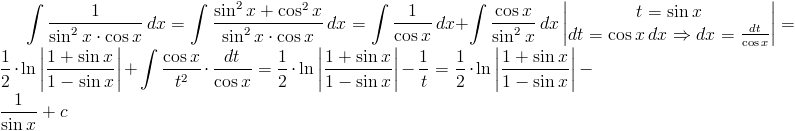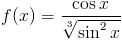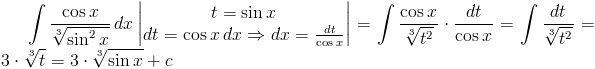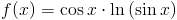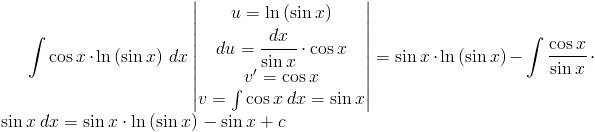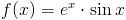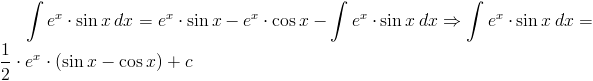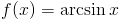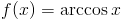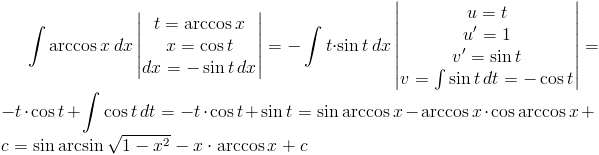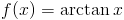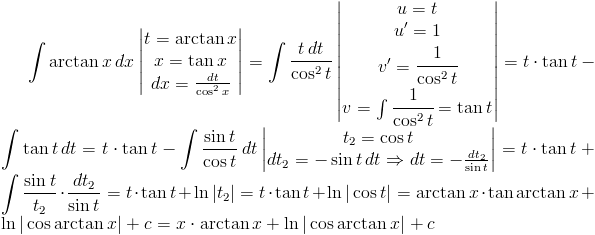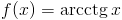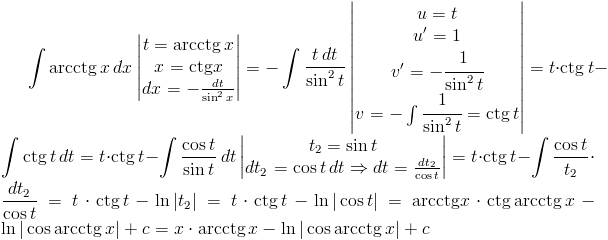Obliczanie całek funkcji trygonometrycznych
Stronę tą wyświetlono już: 7016 razy
Zadanie 1 Obliczyć całkę z następującej funkcji:
Rozwiązanie:
Zadanie 2 Obliczyć całkę z następującej funkcji:
Rozwiązanie:
Zadanie 3 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Pozostało jedynie przekształcenie równości składającej się z ostatniego i pierwszego członu powyższego równania:
Wzór [24] jest tak zwanym wzorem rekurencyjnym rozpisywanym do momentu otrzymania całki z sinusa o potędze 1 lub 0.
Zadanie 4 Stosując wzór [1] obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 5 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Przekształcając pierwszy i ostatni człon powyższego równania tak jak w zadaniu 3 uzyskany zostaje wzór rekurencyjny:
Zadanie 6 Wykorzystując wzór [2] obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 7 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Zadanie 8 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Zadanie 9 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Zadanie 10 Korzystając z wzoru [26] obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 11 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Zadanie 12 Korzystając z wzoru [27] obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 13 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Konieczne będzie użycie wzoru [49] z działu Matematyka: Funkcje: Funkcje trygonometryczne.
Zadanie 14 Wyprowadzić wzór na całkę z funkcji:
Rozwiązanie:
Sprowadzenie do wspólnego mianownika ostatniego członu powyższego równania wymaga takich wartości parametrów A, B, dla których spełnione jest następujące równanie:
Z powyższej równości można ułożyć układ dwóch równań: pierwszego składającego się z czynników przy których stoi zmienna pomocnicza t, oraz drugiego przy którym owa zmienna nie występuje. Układ równań będzie więc wyglądał następująco:
Podstawiając za A, B wyliczone wartości można dokończyć obliczanie całki:
Zadanie 15 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 16 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 17 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 18 Obliczyć całkę z funkcji:
Rozwiązanie:
Konieczne jest zapoznanie się z wzorem [14] z działu Matematyka: Funkcje: Funkcje trygonometryczne.
Zadanie 19 Obliczyć całkę z funkcji:
Rozwiązanie:
Konieczne jest zapoznanie się z wzorem [13] z działu Matematyka: Funkcje: Funkcje trygonometryczne.
Zadanie 20 Obliczyć całkę z funkcji:
Rozwiązanie:
Konieczne jest zapoznanie się z wzorem [15] z działu Matematyka: Funkcje: Funkcje trygonometryczne.
Zadanie 21 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 22 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 23 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 24 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 25 Obliczyć całkę z funkcji:
Rozwiązanie:
Rozwiązanie całki z cos-1x zostało zaczerpnięte z zadania 14.
Zadanie 26 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 27 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 28 Obliczyć całkę z funkcji:
Rozwiązanie:
Przekształcić należy równość, którego lewą stroną jest pierwszy człon powyższego równania natomiast prawą stroną jest człon ostatni.
Zadanie 29 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 30 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 31 Obliczyć całkę z funkcji:
Rozwiązanie:
Zadanie 32 Obliczyć całkę z funkcji:
Rozwiązanie:

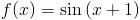
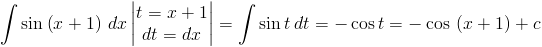
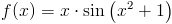

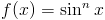
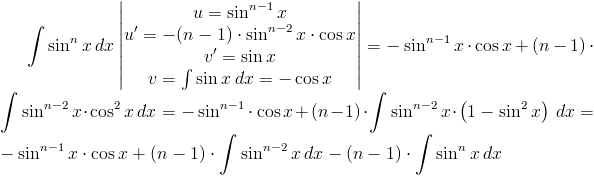
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1389.gif)
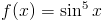
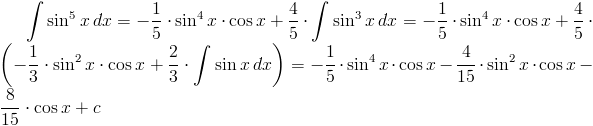
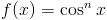
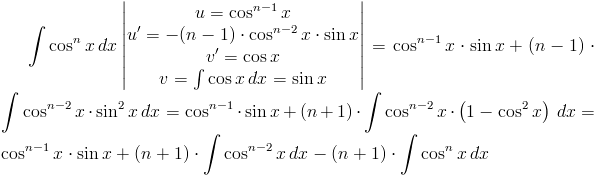
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1394.gif)
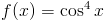
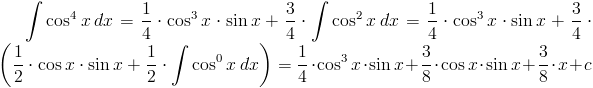
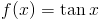
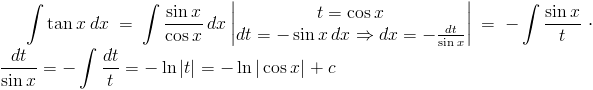
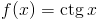
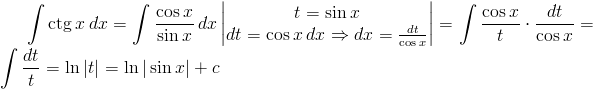

![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1402.gif)
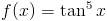
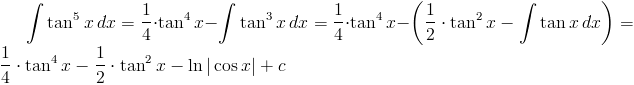
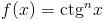
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_1406.gif)

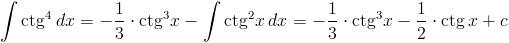
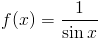
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1410.gif)
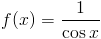
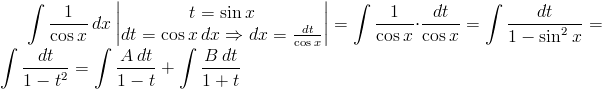
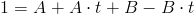
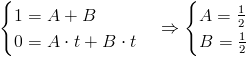
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1416.gif)